Kezdőlap


Feladat:	2003. évi Eötvös fizikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2004/március, 170 - 171. oldal		PDF \| MathML
Témakör(ök):	Folyadékok és gázok egyensúlya, Gördülés lejtőn, Eötvös Loránd (korábban Károly Irén)
Hivatkozás(ok):	Feladatok: 2004/március: 2003. évi Eötvös fizikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Kínálkozik a dinamikai megoldás. A higanyra erőt fejt ki a Föld és a henger. A hengerre erőt fejt ki a Föld, a higany és a lejtő. A (higany + henger) rendszerre tehát a Föld és a lejtő fejtenek ki erőt, melyek következtében a rendszer tömegközéppontja a lejtővel párhuzamos $a$ gyorsulással mozog. $S$ -sel jelölve a hengerre ható súrlódási erőt, a dinamika alaptörvénye szerint

\begin{matrix} (m + M) g sin α - S = (m + M) a . \end{matrix}

A lejtőn csúszásmentesen gördülő henger az ugyancsak

a

gyorsulással mozgó tömegközéppontja körül

β = a / R

szöggyorsulással forog. A gyorsuló forgást az

S

súrlódási erő idézi elő. (Vegyük észre, hogy a higany nem forog, mivel a henger és a higany közötti súrlódás elhanyagolható.) Így a forgásra vonatkozó dinamikai egyenlet: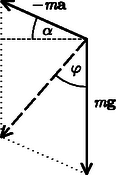

\begin{matrix} S R = M R^{2} \frac{a}{R}, \end{matrix}

amelyből

\begin{matrix} S = M a \end{matrix}

adódik. Ezt a haladó mozgás dinamikai egyenletébe helyettesítve a gyorsulásra kapjuk:

\begin{matrix} a = \frac{m + M}{m + 2 M} g sin α . \end{matrix}

Speciális esetekben:

\begin{matrix} a = {\begin{matrix} g sin α, & ha M ≪ m; \\ \frac{2}{3} g sin α, & ha M = m; \\ \frac{1}{2} g sin α, & ha M ≫ m . \end{matrix} \end{matrix}

A higany felszínének a vízszintessel bezárt szögét legegyszerűbben abból határozhatjuk meg, hogy a folyadék felszíne a folyadékkal együtt mozgó gyorsuló rendszerben is merőleges a rá ható (nehézségi + tehetetlenségi) erők eredőjére. Amekkora

φ

szöget zár be ez az eredő erő a függőlegessel, akkora

φ

szöget fog a higany felszíne a vízszintessel bezárni. A 2. ábra alapján a keresett szög tangense könnyen meghatározható:

\begin{matrix} tg φ = \frac{m a cos α}{m g - m a sin α} = \frac{cos α}{\frac{g}{a} - sin α} . \end{matrix}

2. ábra

Vizsgáljuk meg a gyorsulásra felírt három speciális esetet!

a)

M ≪ m

esetén

\begin{matrix} tg φ = \frac{cos α}{\frac{1}{sin α} - sin α} = tg α, \end{matrix}

vagyis ekkor

φ = α = 10^{\circ}

b)

M = m

esetén

\begin{matrix} tg φ = \frac{cos α}{\frac{3}{2 sin α} - sin α} = \frac{2 sin α cos α}{3 - 2 sin^{2} α}, \end{matrix}

amiből

φ = 6, 636^{\circ} \approx 6, 6^{\circ}

c)

M ≫ m

esetén

\begin{matrix} tg φ = \frac{cos α}{\frac{2}{sin α} - sin α} = \frac{sin α cos α}{2 - sin^{2} α}, \end{matrix}

ahonnan

φ = 4, 962^{\circ} \approx 5, 0^{\circ}

Megjegyzés. A

M ≫ m

eset diszkussziója nem volt feladat, itt csak a szimmetria kedvéért, no meg azért is tárgyaltuk, mert néhány versenyző figyelmetlenségből ezt vizsgálta az

M ≪ m

eset helyett.