Feladat: B.3977 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Fonyó Dávid ,  Kunos Ádám 
Füzet: 2007/szeptember, 338 - 340. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletrendszerek, Pitagorasz-tétel alkalmazásai, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 2007/február: B.3977

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az x,y,z>0 ismeretlenek között nem lehetnek egyenlőek, mert bármely kettő egyenlősége esetén az egyik ismeretlent helyettesítve és kiküszöbölve az egyenletekből ellentmondásra jutunk. Például x=y esetén (1) szerint x=y=23, amit (2)-be, illetve (3)-ba helyettesítve z-re két olyan másodfokú egyenletet kapunk, amelyek bal oldala azonos, a jobb oldalon viszont 5, illetve 3 áll.
Így megszorozhatjuk az egyenleteket rendre (x-y)-nal, (y-z)-vel, (z-x)-szel; a két szám köbének különbségére ismert azonosság révén az

x3-y3=2(x-y),y3-z3=5(y-z),z3-x3=3(z-x)
egyenletekhez jutunk. Ezeket összeadva és x-et kifejezve:
x=3y-2z.(4)
x értékét az (1)-es egyenletbe helyettesítve: (3y-2z)2+(3y-2z)y+y2=2, amiből
13y2-14yz+4z2=2.(5)
Az (5) egyenlet 5-szöröséből kivonva a (2) egyenlet 2-szeresét és a kapott egyenletet 9-cel osztva 7y2-8zy+2z2=0 adódik. Az egyenletet y-ra megoldva:
y1,2=4±27z,(6)
amit a (4)-es egyenletbe helyettesítve:
x1=-2+327z  és  x2=-2-327z,(7)
ahol x2 biztosan negatív, így az x1 és y1 értékekkel folytatva az egyenlet megoldását, ezeket behelyettesítjük az (1) egyenletbe, amiből összevonás után: z2=19-327; mivel z pozitív szám, z=19-327 adódik. A (6) és (7) egyenleteket négyzetre emelve és z2 értékét behelyettesítve, valamint figyelembe véve, hogy x és y is csak pozitív számok lehetnek, az
x=10-627  és  y=6+227
megoldásokat kapjuk. A kapott gyökök kielégítik az egyenletet.
Az x2, y2 és z2 értékének ismeretében az (1), (2) és (3) egyenletek összegét képezve: 2(x2+y2+z2)+(xy+yz+zx)=10, amiből
xy+yz+zx=10-2(x2+y2+z2)==10-2⋅10-62+6+22+19-327=22.
Tehát xy+yz+zx=22.
 
II. megoldás. A keresett xy+yz+xz értéket anélkül is megkaphatjuk, hogy megoldanánk az egyenletrendszert. Vegyük észre, hogy az adott egyenletek a koszinusztételre emlékeztetnek. Ebből kiindulva a feladatnak geometriai értelmezést adhatunk.
Tegyük fel, hogy van az egyenletrendszernek pozitív számokból álló megoldása és legyen ez x, y, z. Vegyünk fel a síkban egy O pontot és az A, B, C pontokat úgy, hogy OA=x, OB=y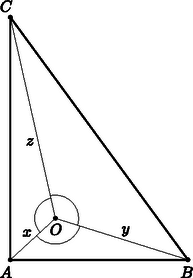, OC=z, AOB∢=BOC∢=COA∢=120∘ legyen.
 
 

Ekkor az AB, BC, CA szakaszok hossza a koszinusztételből és az egyenletrendszerből meghatározható:
AB2=x2+y2-2xycos120∘=x2+y2+xy=2,BC2=y2+z2-2zycos120∘=y2+z2+yz=5,CA2=x2+z2-2xzcos120∘=x2+z2+xz=3.
Tehát ABC egy 2, 3, 5 oldalú háromszög, így Pitagorasz tételének megfordításából adódóan derékszögű.
Számítsuk ki az ABC háromszög területét kétféleképpen: mivel derékszögű, a területe egyrészt a befogói szorzatának a fele, másrészt az AOB, BOC, COA háromszögek területének összege.
AB⋅AC2=2⋅32=xysin(120∘)2+yzsin(120∘)2+zxsin(120∘)2==34(xy+yz+xz),
tehát
2⋅32=34(xy+yz+xz),innenxy+yz+xz=22.

Azt kaptuk tehát, hogy ha van az egyenletrendszernek pozitív számokból álló megoldása, akkor erre xy+yz+xz=22.
Meg kell vizsgálnunk még, hogy van-e az egyenletrendszernek pozitív számokból álló megoldása.
Gondolatmenetünk alapján jól látható, hogy a 2, 3, 5 oldalú derékszögű háromszög izogonális pontját a csúcsokkal összekötő szakaszok hossza megoldása az egyenletrendszernek.