Kezdőlap


Feladat:	B.3930	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Miklós Rozália , Molnár Márton
Füzet:	2007/szeptember, 335 - 336. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Konvex sokszögek, Teljes indukció módszere, Feladat
Hivatkozás(ok):	Feladatok: 2006/szeptember: B.3930

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a csúcsok száma 3, akkor az állítás nyilvánvaló. Egyébként tekintsük az 1. ábrát, melyen bizonyos átlók be vannak húzva. (Az ábrán $k = 12$ , ahol $k$ a csúcsok számát jelöli.)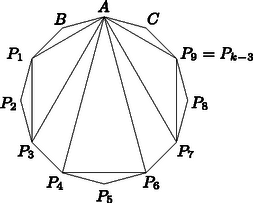

1. ábra

A szabadon választott

A

csúcs két szomszédja legyen

B

és

C

, a többi csúcsot jelölje

P_{n}

. Ez utóbbi csúcsok száma osztható 3-mal.

A

-ból minden olyan

P_{n}

csúcsba fut él, amelyre

n

a 3-mal osztva 0 vagy 1 maradékot ad. Azok a

P_{n}

csúcsok, amelyekbe

A

-ból fut átló, az ábrának megfelelően szintén össze vannak kötve:

P_{1}

‐

P_{3}

P_{4}

‐

P_{6}

stb.
Így

B

C

és az olyan

P_{n}

-ek, melyekre

n

a 3-mal osztva 2 maradékot ad, pontosan egy háromszögnek a pontjai, ezek rendre

A B P_{1}

A C P_{k - 3}

és

P_{n - 1} P_{n} P_{n + 1}

P_{1}

P_{k - 3}

és azok a

P_{n}

csúcsok, melyekre

n

a 3-mal osztva 0, illetve 1 maradékot ad, három, vagyis páratlan sok háromszögben vannak benne. Ezek rendre:

A B P_{1}

A P_{1} P_{3}

P_{1} P_{2} P_{3}

;

A C P_{k - 3}

A P_{k - 3} P_{k - 5}

P_{k - 3} P_{k - 4} P_{k - 5}

;

A P_{n - 2} P_{n}

P_{n - 2} P_{n - 1} P_{n}

A P_{n} P_{n + 1}

;

A P_{n - 1} P_{n}

A P_{n} P_{n + 2}

P_{n} P_{n + 1} P_{n + 2}

.
Végül az

A

csúcs a

P_{n}

csúcsok

\frac{2}{3}

részével van összekötve, így

\frac{2}{3} (k - 3) + 1 = \frac{2}{3} k - 1

háromszögben van benne. Mivel

k

osztható 3-mal,

\frac{2}{3} k

páros, így

A

is páratlan sok háromszögnek csúcsa.

II. megoldás. A feladatot a teljes indukció módszerével oldjuk meg. Legyen a sokszög csúcsainak száma

3 n

n = 1

-re a sokszög háromszög, amire az állítás 0 átló behúzásával teljesül.
Tegyük fel, hogy az állítás igaz

n

-re. Tekintsünk egy

3 n + 3

csúcsú sokszöget.
Ennek egy

3 n

csúcsú része a vastag vonallal jelölt sokszög, melyre a feltevés szerint igaz az állítás. (Ezt a részt úgy kaptuk az eredeti sokszögből, hogy levágtunk belőle három szomszédos csúcsot.) Húzzuk be a szaggatott vonallal jelölt átlókat. Ekkor az

A

és az

E

csúcsoknál történt változás, és keletkezett három új csúcs.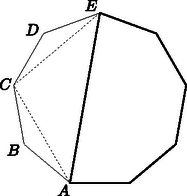

2. ábra

A

és

E

csúcsnál 2-vel több háromszög van, mint eddig, tehát most is páratlan sok háromszögnek a csúcsai.
A

B

és

D

csúcsok egy háromszögnek a pontjai.
Végül a

C

csúcs három háromszögben van benne.
Tehát az állítás

(n + 1)

-re is, vagyis minden csúcsa páratlan sok háromszögnek pontja.