| Feladat: | B.3949 | Korcsoport: 18- | Nehézségi fok: átlagos |
| Füzet: | 2008/február, 96 - 97. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gráfelmélet, Konstruktív megoldási módszer, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2006/november: B.3949 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Mivel minden -re darab -edfokú csúcs van, a gráf csúcsainak fokszám összege ; ez nyilván páros, hiszen éppen az élek számának kétszerese. Az paritása megegyezik az paritásával, tehát paritása megegyezik a paritásával, ami , ezért szükséges, hogy az egymáshoz relatív prím és tényezők valamelyike 4-gyel osztható legyen, vagyis az szám 4-gyel osztva 0 vagy 3 maradékot adjon. Megmutatjuk, hogy ez a feltétel egyben elégséges is. A szóbajövő legkisebb , illetve esetben ilyen gráfot láthatunk a mellékelt ábrán. Ezután elegendő megmutatni, hogy ha valamely -re találtunk egy megfelelő gráfot, akkor értékét 4-gyel növelve, konstruálni tudunk egy megfelelő gráfot is. Ezt úgy tehetjük meg, hogy a gráf mellé felvesszük a , , és teljes gráfokat rendre , , , illetve csúcson úgy, hogy az öt gráf csúcshalmazai páronként diszjunktak legyenek, majd pedig a és gráfok összesen csúcsát egy-egy új él segítségével összepárosítjuk a és gráfok összesen csúcsával. (Tulajdonképpen már a gráfot is megkaphatjuk ilyen módon a 0 szögpontú üres gráfból.) Ezzel a -hez tartozó csúcsok fokszáma nem változik; a , , és gráfok csúcsainak foka eredetileg rendre , , és , a párosítások révén ezek a fokszámok 1-gyel nőnek, tehát az új gráf az , , , fokokra is teljesíti a feladat feltételét, -nél magasabb fokú pontot pedig nem tartalmaz. 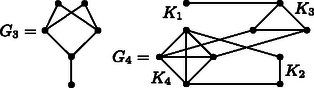 Megjegyzés. A konstrukció szerint esetén két komponensből áll. Felmerül a kérdés, hogy található-e összefüggő konstrukció. A válasz igen. |