Kezdőlap


Feladat:	B.3948	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Lovas Lia Izabella , Somogyi Ákos , Szalóki Dávid
Füzet:	2008/február, 93 - 96. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Harmadfokú függvények, Szélsőérték differenciálszámítással, Feladat
Hivatkozás(ok):	Feladatok: 2006/november: B.3948

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Alakítsuk át a vizsgált polinomot.

\begin{matrix} 3 a^{5} b - 40 a^{3} b^{3} + 48 a b^{5} = a b (3 a^{4} - 40 a^{2} b^{2} + 48 b^{4}) = a b (3 {(a^{2} + 4 b^{2})}^{2} - 64 a^{2} b^{2}) . \end{matrix}

a^{2} + 4 b^{2} = 4

feltételt kihasználva a kifejezés tovább alakítható:

\begin{matrix} a b (3 {(a^{2} + 4 b^{2})}^{2} - 64 a^{2} b^{2}) = a b (48 - 64 a^{2} b^{2}) . \end{matrix}

a^{2}

és

4 b^{2}

nyilván nemnegatív, így felírható rájuk a számtani és mértani közép közötti egyenlőtlenség:

\begin{matrix} \sqrt[]{4 a^{2} b^{2}} \leq \frac{a^{2} + 4 b^{2}}{2}, amiből | 2 a b | \leq \frac{4}{2} \end{matrix}

és így

| a b | \leq 1

.
Legyen

a b = x

. Ekkor a kifejezés a

- 64 x^{3} + 48 x

formát ölti. Akkor tudnánk függvényvizsgálatot végezni, ha ez a kifejezés valóban függvény, vagyis ha minden

- 1 \leq x \leq 1

értékhez találunk olyan

a

és

b

számot, amelyekre fennáll, hogy

a^{2} + 4 b^{2} = 4

és

a b = x

.
Ha

- 1 \leq a b = x \leq 1

, akkor

a \neq 0

esetén

b = \frac{x}{a}

-t behelyettesítve a feltételbe:

\begin{matrix} a^{2} + 4 \cdot \frac{x^{2}}{a^{2}} = 4, amiből a^{4} - 4 a^{2} + 4 x^{2} = 0. \end{matrix}

Ezt

a^{2}

-re megoldva:

\begin{matrix} a^{2} = \frac{4 \pm \sqrt[]{16 - 16 x^{2}}}{2} = 2 \pm 2 \sqrt[]{1 - x^{2}} . \end{matrix}

Ez pontosan akkor nemnegatív, ha

1 - x^{2} \geq 0

, vagyis ha

| x | \leq 1

. Ekkor tehát van megfelelő

a

és

b

. Ha pedig

a = 0

(ez

x = 0

mellett jön szóba), akkor

b = 1

jó.
Tehát az

\begin{matrix} f (x) = - 64 x^{3} + 48 x = x (- 64 x^{2} + 48) \end{matrix}

függvényt vizsgáljuk a

[- 1; 1]

intervallumon. A függvény páratlan, zérushelyei

\begin{matrix} x = 0, illetve x = \pm \frac{\sqrt[]{3}}{2} . \end{matrix}

A függvény deriváltja:

f' (x) = - 192 x^{2} + 48

, ennek zérushelyei

x = \pm \frac{1}{2}

. A derivált előjele alapján

x = - \frac{1}{2}

minimum,

x = \frac{1}{2}

maximum. A fentiek alapján a függvény vázlatos képe az ábrán látható.

A helyi minimum értéke:

\begin{matrix} f (- \frac{1}{2}) = - 64 \cdot {(- \frac{1}{2})}^{3} + 48 \cdot (- \frac{1}{2}) = - 16. \end{matrix}

Meg kell nézni, hogy a vizsgált intervallum szélén,

x = 1

-nél nem kisebb-e a függvényérték:

f (1) = - 64 + 48 = - 16

. A két érték megegyezik.
A helyi maximum értéke:

\begin{matrix} f (\frac{1}{2}) = - 64 \cdot {(\frac{1}{2})}^{3} + 48 \cdot (\frac{1}{2}) = 16. \end{matrix}

A vizsgált intervallum szélén:

f (- 1) = - 64 \cdot (- 1) + 48 \cdot (- 1) = 16

.
Így

- 16 \leq 3 a^{5} b - 40 a^{3} b^{3} + 48 a b^{5} \leq 16

, és a kifejezés a

[- 16; 16]

intervallum minden értékét fölveszi.

II. megoldás. Mivel

a^{2} + 4 b^{2} = 4

, így

{(\frac{a}{2})}^{2} + b^{2} = 1

. Ez azt jelenti, hogy a derékszögű koordináta-rendszerben az

(\frac{a}{2}; b)

koordinátájú pont illeszkedik a

(0; 0)

középpontú, egységsugarú körre. Mivel ezen kör bármely pontja megfelelő

x \in R

esetén

(sin x; cos x)

koordinátákkal rendelkezik, így bármely feladatbeli

(\frac{a}{2}; b)

számpárhoz található olyan

x \in [0; 2 π [

, melyre

\frac{a}{2} = sin x

és

b = cos x

. Válasszuk ezt a megfeleltetést. Ekkor

a = 2 sin x

és

b = cos x

.
Alakítsuk át a feladatbeli kifejezést a következő módon:

\begin{matrix} P (a; b) & : = & 3 a^{5} b - 40 a^{3} b^{3} + 48 a b^{5} = a b (3 a^{4} - 40 a^{2} b^{2} + 48 b^{4}) = \\ = & a b (3 {(a^{2} + 4 b^{2})}^{2} - 64 a^{2} b^{2}) = a b (3 \cdot 4^{2} - 64 a^{2} b^{2}) = 16 a b \cdot (3 - 4 a^{2} b^{2}) . \end{matrix}

a b = 2 sin x cos x = sin 2 x

összefüggést figyelembe véve:

\begin{matrix} P (a; b) & = & 16 sin 2 x (3 - 4 sin^{2} 2 x) = 16 sin 2 x (3 (sin^{2} 2 x + cos^{2} 2 x) - 4 sin^{2} 2 x) = \\ = & 16 sin 2 x (2 cos^{2} 2 x + cos^{2} 2 x - sin^{2} 2 x) = 16 sin 2 x (2 cos^{2} 2 x + cos 4 x) = \\ = & 16 (2 sin 2 x cos 2 x cos 2 x + cos 4 x sin 2 x) = \\ = & 16 (sin 4 x cos 2 x + cos 4 x sin 2 x) = 16 (sin (4 x + 2 x)) = 16 sin 6 x . \end{matrix}

Azt kaptuk, hogy

3 a^{5} b - 40 a^{3} b^{3} + 48 a b^{5} = 16 sin 6 x

. Mivel

- 1 \leq sin 6 x \leq 1

, azért

\begin{matrix} - 16 \leq 3 a^{5} b - 40 a^{3} b^{3} + 48 a b^{5} = 16 sin 6 x \leq 16. \end{matrix}

Mivel

- 16 \leq 16 sin x \leq 16

, és

a = 2 sin x

, valamint

b = cos x

, a

P (a; b)

értéke a

[- 16; 16]

intervallum bármely eleme lehet.
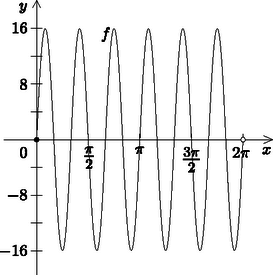
Ábrázoljuk az

f (x) = 16 sin 6 x

függvényt a

[0; 2 π [

intervallumon.

Hat olyan

x

érték van, amelyre a függvény felveszi a maximumát, ezek mindegyikéhez tartozik egy-egy

(a; b)

értékpár.
A minimális értéket szintén hat helyen veszi föl, minden más értéket pedig tizenkét helyen.

Megjegyzés. 1. Az I. megoldásban

| x | < 1

esetén négy megfelelő

a

értéket kapunk, így négy

(a; b)

értékpár tartozik egy

x

értékhez. Mivel

- 16 < y < 16

esetén három

x

-re is teljesül, hogy

f (x) = y

, a vizsgált kifejezés minden

- 16 < y < 16

számot

3 \cdot 4 = 12

megfelelő

(a; b)

esetén vesz föl. A minimumot és a maximumot pedig

4 + 2 = 6

esetben, hiszen

x = 1

és

x = - 1

esetén egyaránt két-két megfelelő

(a; b)

számpár van.
2. A feladat szövegét többféleképpen is lehetett érteni: a ,,Milyen nagy lehet'' kérdést volt, aki úgy értelmezte, hogy csak a kifejezés maximumát kell megkeresni.