Feladat: 2007. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2008/február, 69 - 70. oldal  PDF  |  MathML 
Témakör(ök): Négyzetrács geometriája, Részhalmazok, Indirekt bizonyítási mód, Teljes indukció módszere, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 2008/február: 2007. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. megoldás. Azt mondjuk, hogy K' a H megengedett részhalmaza, ha K'-nek minden függőleges egyenesen legfeljebb két pontja van (tehát vízszintes egyenesen lehet akár több is), és a K' pontjait összekötő tengelypárhuzamos szakaszok lefedik H minden pontját. Létezik megengedett halmaz: ilyen K'-t alkotnak például H mindazon pontjai, amelyek a saját függőleges egyenesükön legalsók vagy legfelsők, hiszen ekkor már a K' pontjai meghatározta függőleges szakaszok lefedik H minden pontját.
Legyen K egy olyan megengedett halmaz, amelyre a K pontjait összekötő függőleges (esetleg ponttá fajuló) zárt szakaszok által lefedett H-beli pontok száma minimális. Állítjuk, hogy ez a K kielégíti a feladat követelményeit. A K halmaz megengedettsége miatt mindössze azt kell belátnunk, hogy K-nak minden vízszintes egyenesen legfeljebb két pontja van.
Indirekt bizonyítunk. Tegyük fel, hogy K három pontja, mondjuk p, q és r egy vízszintes egyenesre esnek úgy, hogy a q a p és az r között van. Ha a q pontot tartalmazó függőleges egyenesen K-nak nincs más pontja, akkor legyen K'=K∖{q}. Ha van, akkor pontosan egy van (mondjuk s). Legyen q' a qs nyílt félegyenesnek a q végponthoz legközelebbi H-beli pontja (ilyen van, mert s∈K⊆H), és legyen K'=K∖{q}∪{q'}. Mindkét esetben K'⊆H, K'-nek minden függőleges egyenesen legfeljebb két pontja van, és a K' pontjait összekötő tengelypárhuzamos szakaszok lefedik H∖K' minden pontját. Ráadásul a K' pontjait összekötő függőleges (esetleg ponttá fajuló) zárt szakaszok által lefedett H-beli pontok száma kisebb, mint ugyanez a szám a K esetén. Ez nem lehetséges.
A kapott ellentmondás igazolja, hogy a K halmaz a feladatban megfogalmazott mindkét feltételt teljesíti.  □

 

A fenti érvelés bár igazolja a feladat állítását, nem ad jól használható algoritmust egy megfelelő K halmaz megtalálására. Az alábbi megoldás ezzel is szolgál.
 
2. megoldás. A H halmaz mérete szerinti indukcióval bizonyítunk. Világos, hogy ha |H|=1, akkor K=H teljesíti a feladatbeli feltételeket. Tegyük fel, hogy legfeljebb n pontú H halmazra már igazoltuk az állítást, és legyen a H halmaznak n+1 pontja.
Alkossák a K* halmazt a H azon pontjai, amelyek a saját függőleges egyenesükön legalsók vagy legfelsők. Világos, hogy K* teljesíti a feladat (b) feltételét. Ha az (a) feltétel is teljesül K*-ra, akkor készen vagyunk: K=K* megfelelő. Ha azonban az (a) feltétel nem teljesül, akkor ennek az az oka, hogy van K*-nak olyan q pontja, hogy a q vízszintes egyenesén q-tól balra és jobbra is van K*-nak pontja, mondjuk p és r.
Az indukciós feltevés szerint az n pontú H∖{q} halmaznak létezik olyan K részhalmaza, ami minden tengelypárhuzamos egyenesen legfeljebb két pontot tartalmaz, és H∖{q} minden pontját lefedik a K által meghatározott tengelypárhuzamos szakaszok. Állítjuk, hogy ugyanez a K halmaz H-hoz is megfelelő. Ehhez elegendő azt belátnunk, hogy q rajta van egy K-beli végpontokkal rendelkező vízszintes szakaszon. Vizsgáljuk a p pontot! Mivel p egy függőleges egyenes H-beli legalsó vagy legfelső pontja, azért vagy p∈K, vagy p egy K-végpontú vízszintes szakaszon található, tehát q vízszintes egyenesén van p-től balra K-nak pontja. Hasonlóan, ha r∉K, akkor r is csak egy K meghatározta vízszintes szakaszon lehet, így K-nak r-től jobbra is van pontja. Azt kaptuk, hogy q csakugyan egy K végpontú vízszintes szakasz belsejében van, tehát K valóban megfelel a feladat feltételeinek, vagyis az állítás n+1 pontú halmazokra is igaz. Ezzel az indukciós lépést igazoltuk, a bizonyítást befejeztük.  □
 
Megjegyzések. 1. A 2. megoldásból úgy kaphatunk hatékony algoritmust a K halmaz keresésére, hogy első lépésben képezzük a K* halmazt. Ha K* nem alkalmas K-nak a bizonyításbeli q pontja miatt, akkor a H∖{q} halmazra rekurzívan meghívjuk ugyanezt az algoritmust. Így legfeljebb |H|-1 alkalommal képezve a megfelelő K* halmazt, előbb-utóbb egy keresett K-t kapunk. (Az is könnyen látható, hogy nem kell egyenként elhagyni a q pontokat: megtehetjük azt is, hogy H-ból egyszerre hagyjuk el K* összes olyan pontját, ami K*-beli végpontokkal rendelkező vízszintes szakasz belsejében van. Így az algoritmus gyorsabban végetér.)
2. Több hamis bizonyítás érkezett a feladatra. Legtöbbjük módszeréből az is következne, hogy tetszőleges H halmazhoz egyértelműen létezik a keresett K. A példa mutatja, hogy ez koránt sincs így.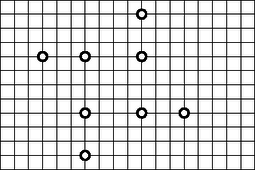
 
 

3. Érdekes tulajdonsága a fenti megoldásokban konstruált K halmaznak, hogy ha egy K' halmaz rendelkezik a feladatbeli (a) és (b) tulajdonságokkal, akkor minden K'-beli végpontokkal rendelkező függőleges szakasz része egy K meghatározta függőleges szakasznak, továbbá minden K meghatározta vízszintes szakasz része egy K'-beli végpontokkal rendelkező vízszintes szakasznak. Más szóval K a ,,legmagasabb'' és egyben ,,legkeskenyebb'' a kívánt tulajdonságú halmazok között. Természetesen ha a 90∘-kal elforgatott ábrán végezzük el a konstrukciót (azaz a függőleges és vízszintes szavakat felcseréljük a bizonyításban), akkor a ,,legalacsonyabb'' és ,,legszélesebb'' megoldást kapjuk meg.
4. A feladat szoros rokonságot mutat Gale és Shapley (sajnos nem eléggé) ismert ,,stabil házassági'' tételével.