Kezdőlap


Feladat:	B.4008	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Éles András
Füzet:	2007/december, 542 - 543. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Párhuzamos szelők tétele és megfordítása, Pitagorasz-tétel alkalmazásai, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 2007/május: B.4008

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel $ctg 70^{\circ} = \frac{cos 70^{\circ}}{sin 70^{\circ}}$ , így a bizonyítandó egyenlőség ekvivalens a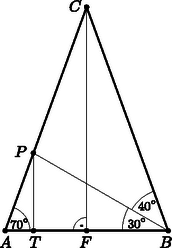

\begin{matrix} cos 70^{\circ} + 4 cos 70^{\circ} sin 70^{\circ} = \sqrt[]{3} sin 70^{\circ} \end{matrix}

egyenlettel.

2 cos 70^{\circ} sin 70^{\circ} = sin 140^{\circ}

, ezt beírva, 2-vel osztva és rendezve:

\begin{matrix} sin 140^{\circ} = \frac{\sqrt[]{3}}{2} sin 70^{\circ} - \frac{1}{2} cos 70^{\circ} . \end{matrix}

Mivel

\frac{\sqrt[]{3}}{2} = cos 30^{\circ}

és

\frac{1}{2} = sin 30^{\circ}

, az addíciós tételt felhasználva

\begin{matrix} cos 30^{\circ} sin 70^{\circ} - sin 30^{\circ} cos 70^{\circ} = sin (70^{\circ} - 30^{\circ}) = sin 40^{\circ}, \end{matrix}

ami valóban

sin 140^{\circ}

, hiszen minden

α

-ra

sin (180 - α) = sin α

II. megoldás. A feladat a

70^{\circ}

-os szögről szól. Vegyünk fel egy egyenlő szárú háromszöget, melynek alapon lévő szögei

70^{\circ}

-osak. Így geometriai értelmezést adhatunk a feladatnak. Legyen

P

a háromszög

A C

szárán az a pont. melyre

A B P ∢

30^{\circ}

-os. Állítsunk merőlegest a

P

pontból az

A B

alapra, a talppont legyen

T

A B

felezőpontja pedig az

F

pont.

Legyen

P T = 1

, ekkor

\begin{matrix} P B = \frac{P T}{sin 30^{\circ}} = 2, T B = P B \cdot cos 30^{\circ} = \sqrt[]{3}, \\ \frac{A T}{P T} = ctg 70^{\circ} . \end{matrix}

Legyen

x = A T = P T \cdot ctg 70^{\circ} = ctg 70^{\circ}

.
Az

A T P

háromszögben a Pitagorasz-tételt használva:

A P = \sqrt[]{x^{2} + 1}

\begin{matrix} A B = A T + T B = x + \sqrt[]{3}, A F = \frac{A B}{2} = \frac{x + \sqrt[]{3}}{2}, \\ T F = A F - A T = \frac{x + \sqrt[]{3}}{2} - x = \frac{\sqrt[]{3} - x}{2} . \end{matrix}

B P C

háromszög egyenlő szárú, így

P C = P B = 2

.
A párhuzamos szelők tételének következménye szerint:

\begin{matrix} \frac{A T}{A P} = \frac{T F}{P C}, azaz \frac{x}{\sqrt[]{x^{2} + 1}} = \frac{\sqrt[]{3} - x}{4} . \end{matrix}

Vagyis sikerült belátnunk, hogy ha

x = ctg 70^{\circ}

, akkor

\begin{matrix} x + 4 \cdot \frac{x}{\sqrt[]{x^{2} + 1}} = \sqrt[]{3} . \end{matrix}

Mivel

cos 70^{\circ} = \frac{A T}{A P} = \frac{x}{\sqrt[]{x^{2} + 1}}

, azért ez éppen a bizonyítandó állítás:

\begin{matrix} ctg 70^{\circ} + 4 cos 70^{\circ} = \sqrt[]{3} . \end{matrix}