Kezdőlap


Feladat:	B.3865	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Anda Roland , Balambér Dávid , Bogár Péter , Bus Norbert , Csaba Ákos , Csima Géza , Csorba János , Gaál Zsuzsanna , Gaizer Tünde , Gresits Iván , Gyüre Balázs , Klimaj Zoltán , Kovács Péter , Kristóf Panna , Kunovszki Péter , Lovász László Miklós , Mercz Béla , Nagy-Baló András , Németh Kitti Noémi , Pálovics Róbert , Peregi Tamás , Prõhle Zsófia , Salát Zsófia , Ta Phuong Linh , Tossenberger Anna , Udvari Balázs , Vajsz Tibor , Véges Márton
Füzet:	2007/december, 532 - 533. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszögek hasonlósága, Háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2005/december: B.3865

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mivel $A \neq D$ , az $A$ , $B_{1}$ , $B_{2}$ pontok nem esnek egy egyenesre, ahogyan az $A$ , $C_{1}$ , $C_{2}$ pontok sem. Tehát az $A B_{1} B_{2}$ és $A C_{1} C_{2}$ háromszögek valóban léteznek. Vegyük az eredeti háromszögek körüljárási irányát pozitívnak. Szükség esetén az indexeket felcserélve feltehetjük, hogy az $A B_{1} C_{1}$ háromszöget $A$ körüli $φ$ szögű forgatva nyújtás viszi az $A B_{2} C_{2}$ háromszögbe, ahol $0 < φ < π$ . Legyen a $B_{1} A C_{1}$ és $B_{2} A C_{2}$ irányított szögek nagysága $α$ , továbbá a hasonlóság miatt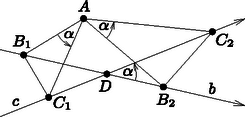

\begin{matrix} \frac{C_{1} A}{B_{1} A} = \frac{C_{2} A}{B_{2} A} = λ . \end{matrix}

Ekkor az

A B_{1} B_{2}

háromszöget

A

körüli,

α

szögű,

λ

arányú forgatva nyújtás viszi az

A C_{1} C_{2}

háromszögbe, ami az első állítást igazolja. Ugyanez a forgatva nyújtás az 1. ábrán feltüntetett

b = B_{1} B_{2}

irányított egyenest a

c = C_{1} C_{2}

irányított egyenesbe viszi. Ezeket a

D

pont két részre osztja, melyeket nevezzünk értelemszerűen bal, illetve jobb oldali résznek.

1. ábra

A második állítás igazolásához (2. ábra) vegyük figyelembe, hogy az

A B_{1} B_{2}

és

A C_{1} C_{2}

háromszögek körüljárási iránya is pozitív. Elegendő azt bizonyítani, hogy az

A

B_{1}

C_{1}

és

D

pontok egy körön vannak. Ez nyilvánvaló, ha

B_{1}

vagy

C_{1}

egybeesik

D

-vel. Az nem lehet, hogy

B_{1}

b

egyenes jobb oldali részén, ugyanakkor

C_{1}

c

egyenes bal oldali részén helyezkedik el, ekkor ugyanis az

A B_{1} C_{1}

háromszög negatív körüljárású lenne. Így három esetet különböztethetünk meg. Az 2. ábrán látható első esetben mindkét pont a megfelelő egyenes bal oldali részén helyezkedik el. Ekkor az

A

és

D

pontok a

B_{1} C_{1}

egyenesnek ugyanazon oldalára esnek, és a

B_{1} C_{1}

szakasz mindkettőből

α

szög alatt látszik, vagyis az állítás következik a kerületi szögek tételének megfordításából. Ehhez teljesen hasonlóan igazolható az állítás abban az esetben is, ha mindkét pont a megfelelő irányított egyenes jobb oldalán van (3. ábra). Végül, ha

B_{1}

b

bal oldali,

C_{1}

pedig

c

jobb oldali részén van, akkor a

B_{1} C_{1}

egyenes elválasztja az

A

és

D

pontokat. Ekkor azonban a

B_{1} C_{1}

szakasz

D

-ből

(π - α)

szög alatt látszik, vagyis az

A B_{1} D C_{1}

négyszög húrnégyszög (4. ábra).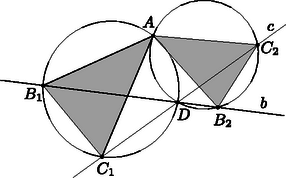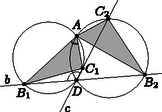

2. ábra

3. ábra

4. ábra