Feladat: C.839 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 2006/október, 404 - 406. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül, Konvex négyszögek, Pitagorasz-tétel alkalmazásai, C gyakorlat
Hivatkozás(ok):Feladatok: 2006/január: C.839

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelöljük a négyszög oldalait a, b, c és d-vel, az átlók metszéspontja által kapott szakaszokat x, y, u és v-vel, az ábra szerint.

 
 

A kapott derékszögű háromszögek oldalaira írjuk fel a Pitagorasz-tételt:
x2+v2=a2,y2+u2=c2,x2+u2=b2,y2+v2=d2.
Az első két egyenletből:
v2-u2=a2-b2,
a másik kettőből:
v2-u2=d2-c2.
A bal oldalak egyenlőségéből következik a jobb oldalak egyenlősége, azaz
a2-b2=d2-c2.
Innen
d2=a2+c2-b2.
Úgy kell tehát megválasztanunk az adott oldalakat, hogy d2>0 legyen.
Ez két esetben teljesül: ha 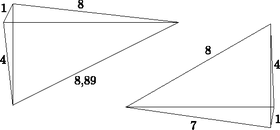a=8, c=4 és b=1, ekkor
d=64+16-1=79≈8,89;
vagy a=8, c=1 és b=4, ekkor
d=64+1-16=7.
Ilyen négyszögek valóban léteznek, ezt mi nem bizonyítjuk, bár ez hozzátartozna a feladat megoldásához. Ezt versenyzőinktől sem vártuk el.
 
 

 
Megjegyzések. 1. A megoldások lényegében azt használták fel, hogy a merőleges átlójú négyszögek esetében a szemközti oldalpárok hosszainak négyzetösszege ugyanannyi. (Ha az oldalak ebben a sorrendben a, b, c, d, akkor a2+c2=b2+d2.) Ebből az összefüggésből számolták ki a negyedik oldalt.
Ahhoz, hogy az összefüggés alapján meghatározott négyszög átlói merőlegesek, azt is be kellene látni, hogy az a2+c2=b2+d2 összefüggésből következik az átlók merőlegessége. Legyenek A, B, C, D a négyszög csúcsai és legyen AC az egyik átló. A B és D csúcsokból erre bocsátott merőlegesek talppontja legyen P és Q úgy, hogy P van az A-hoz közelebb. Legyen |AP|=x, |PQ|=z és |QB|=y. A talppontoknak a megfelelő csúcstól mért távolságai legyenek u és v. Ekkor Pitagorasz tétele szerint a szemköztes oldalpárok hosszának négyzetösszegei x2+u2 és y2+v2, illetve (x+z)2+v2 és (z+y)2+u2. Így az
(x2+u2)+(y2+v2)=((x+z)2+v2)+((z+y)2+u2)
egyenlőséget nyerjük. Ebből 0=2z(x+y)+2z2 következik. Innen z=0, vagyis a két merőleges talppontja egybeesik, tehát a két átló merőleges egymásra.
2. Könnyen belátható, hogy a fenti gondolatmenet konkáv négyszög esetében is alkalmazható.
3. A keresett d oldallal szemben elvileg a, b, c bármelyike lehetne. A szimmetria miatt ez három megoldást adhatna. Ha például a van szemben, akkor d2=b2+c2-a2. Ez kell, hogy pozitív legyen, mert d2>0. A b2+c2-a2 kifejezés biztosan pozitív, hacsak nem a>b,c. Ebben az esetben is pozitív, amennyiben a2<b2+c2. Ez azt is jelentheti, hogy a2, b2, c2 egy háromszög oldalai. Ekkor van három eset; egyébként kettő.