Kezdőlap


Feladat:	C.882	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Czotter Eszter , Miklósi Nikoletta , Prok Tamás
Füzet:	2007/november, 479 - 480. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Oldalak aránya és szögek közötti kapcsolat, Derékszögű háromszögek geometriája, C gyakorlat
Hivatkozás(ok):	Feladatok: 2007/január: C.882

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szögfüggvények tulajdonságai alapján $cos α = sin (90^{\circ} - α)$ . Ezt és az ábra jelöléseit felhasználva:

\begin{matrix} \frac{cos δ}{a} + \frac{sin δ}{b} = \frac{sin (90^{\circ} - δ)}{a} + \frac{sin δ}{b} = \frac{\frac{y}{d}}{a} + \frac{\frac{x}{d}}{b} . \end{matrix}

(2)

A P T

és az

A B C

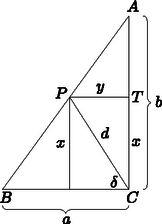háromszögek hasonlóak, és így

\begin{matrix} \frac{T P}{C B} = \frac{A T}{A C}, vagyis \frac{y}{a} = \frac{b - x}{b} . \end{matrix}

Innen

y = \frac{b - x}{b} \cdot a

.
Ezt felhasználva (2) jobb oldala tovább alakítható:

\begin{matrix} \frac{\frac{y}{d}}{a} + \frac{\frac{x}{d}}{b} = \frac{\frac{\frac{b - x}{b} \cdot a}{d}}{a} + \frac{\frac{x}{d}}{b} = \frac{b - x}{b d} + \frac{x}{b d} = \frac{b}{b d} = \frac{1}{d} . \end{matrix}

Ezzel az állítást igazoltuk.

Megjegyzés. Sokan nem a hasonlóságot, hanem a

C P B

és az

A C P

háromszögekre felírt szinusz-tételt használták fel az állítás bizonyításához.

II. megoldás. Az (1) egyenlet mindkét oldalát

a b d

-vel szorozva azt kapjuk, hogy

a b = b d \cdot cos δ + a d \cdot sin δ

. A bal oldalon álló kifejezés a derékszögű háromszög területének kétszerese. Ha belátjuk, hogy a jobb oldalon is a terület kétszerese áll, akkor készen vagyunk.
A szögfüggvények közti összefüggés szerint

cos δ = sin (90^{\circ} - δ)

, így az egyenlet jobb oldala a következőképpen alakul: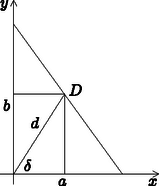

\begin{matrix} b d \cdot sin (90^{\circ} - δ) + a d \cdot sin δ . \end{matrix}

Ez valóban a háromszög területének a kétszerese, ugyanis a

C B P

háromszög területe

\frac{a d \cdot sin δ}{2}

, a

C A P

háromszög területe pedig

\begin{matrix} \frac{b d \cdot sin (90^{\circ} - δ)}{2} = \frac{b d cos δ}{2} . \end{matrix}

Ezzel a bizonyítást befejeztük.

III. megoldás. Helyezzük el a derékszögű háromszöget a koordinátarendszerben úgy, hogy a derékszög csúcsa az origóban legyen. Ekkor az átfogó egyenlete:

\begin{matrix} \frac{x}{a} + \frac{y}{b} = 1. \end{matrix}

D

pont koordinátái

(d cos δ; d sin δ)

Mivel

D

illeszkedik az átfogóra, koordinátái kielégítik az átfogó egyenesének egyenletét, vagyis:

\begin{matrix} \frac{d cos δ}{a} + \frac{d sin δ}{b} = 1. \end{matrix}

Az egyenlet mindkét oldalát

d

-vel osztva éppen a bizonyítandó állításhoz jutunk.