Feladat: A.383 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bogár Péter ,  Hujter Bálint ,  Jankó Zsuzsanna ,  Kisfaludi-Bak Sándor ,  Nagy Csaba ,  Paulin Roland ,  Tomon István 
Füzet: 2006/április, 223 - 227. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Körök, Húrnégyszögek, Nehéz feladat
Hivatkozás(ok):Feladatok: 2005/november: A.383

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A diszkusszió elkerülése érdekében mindenhol irányított szögeket fogunk használni. Az XYZ∢ jelölés azt fogja jelenteni, hogy az XY egyenest mekkora szöggel kell pozitív irányban elforgatni, hogy az YZ egyenest kapjuk. A szög természetesen csak ,,modulo 180∘'' értelemben egyértelmű; két szöget azonosnak tekintünk, ha a különbségük a 180∘-nak többszöröse.
Először kimondjuk az irányított szögek néhány alapvető tulajdonságát, köztük néhány, az iskolából is jól ismert tételt, amelyet alkalmazni fogunk.

(1)Ha P, A, A', illetve P, B, B' kollineáris pontok a síkon, akkor
APB∢=A'PB'∢.
(2)APB∢+BPC∢=APC∢, speciálisan APB∢=-BPA∢.
(3)Az ABC háromszögben ABC∢+BCA∢+CAB∢=0.
(4)Az ABC háromszögben AB=AC akkor és csak akkor teljesül, ha
ABC∢=BCA∢.
(5)Rögzített φ≠0 mellett azon P pontok mértani helye a síkon, melyekre APB∢=φ, egy A-n és B-n átmenő kör. Speciálisan A, B, C, D pontok akkor és csak akkor illeszkednek egy körre, ha ACB∢=ADB∢.

Térjünk most rá a bizonyításra. Jelöljük k középpontját O-val, az AB és ℓ egyenesek metszéspontja legyen M. Húzzunk párhuzamost ℓ-lel B-n keresztül, jelöljük ezt ℓ'-vel, és legyen CE és ℓ' metszéspontja C'. A C'-ből húzott érintők egyenlő hosszúságúak, tehát C'E=C'B. Az EC'B egyenlő szárú háromszöget E-ből középpontosan nagyítva kapjuk, hogy CE=CF (1. ábra).
 

 
1. ábra
 

Legyen a C középpontú, E-n átmenő kör k'. A k kör pontjaira alkalmazva (5)-öt kapjuk, hogy EGF∢=EGA∢=EBA∢=EBO∢. Az OEB egyenlő szárú háromszögben EBO∢=OEB∢, így EGF∢=OEB∢=OEF∢. Ez utóbbi a k' érintőszárú kerületi szöge, hiszen OE és CE merőlegesek. Tehát az EGF∢ éppen a k' kör pontjainál adódó szöggel egyenlő, így a k' kör G-n is átmegy. Tehát CE=CF=CG, így CE és CG a C-ből a k-hoz húzott két érintő (2. ábra).
 

 
2. ábra
 

A BMFG húrnégyszög, mert két szemközti szöge derékszög. (5)-öt alkalmazva erre a négy pontra is (3. ábra),
CFG∢=MFA∢=90∘-FAM∢=90∘-GAB∢==90∘-GDB∢=ADB∢-GDB∢=ADG∢=CDG∢.
Tehát (5) szerint C, F, G, D egy körre illeszkednek.
 

 
3. ábra
 

Jelöljük DF és k második metszéspontját G'-vel, és legyen GAB∢=GDB∢=φ (4. ábra). A CFGD húrnégyszögből, az AMF derékszögű háromszögből és a CFG egyenlő szárú háromszögből: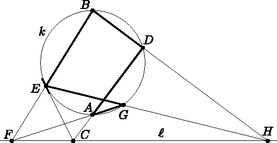
GDG'∢=GDF∢=GCF∢=-2CFG∢=-2(90∘-FAM∢)=2φ=2GAB∢.
A DB egyenes tehát felezi a GDG' szöget, vagyis a B pont felezi a GG' ívet.
 

 
4. ábra
 

 
II. megoldás. Jelöljük H-val a BD és EG egyenesek metszéspontját, és alkalmazzuk a Pascal-tételt az EEBDAG elfajult húrhatszögre (5. ábra). A szemközti oldalak metszéspontja C, F, illetve H (az EE oldal a körhöz E-ben húzott érintő); a Pascal-tétel szerint ez a három pont egy egyenesen van. Tehát a H pont is illeszkedik az ℓ egyenesre.
 

 
5. ábra
 

Legyen G' a k kör és DF másik metszéspontja, és alkalmazzuk most a Pascal-tételt a GG'DBBE elfajult hatszögre (6. ábra). Az F és a H pont két-két szemközti oldal metszéspontja, ezért a harmadik oldalpár, vagyis a GG' egyenes és a k-hoz B-ben húzott érintő metszéspontja is az FH=ℓ egyenesen van. Mivel az érintő párhuzamos ℓ-lel, ez csak akkor lehetséges, ha GG' is párhuzamos velük, tehát G és G' az AB átmérőre szimmetrikus.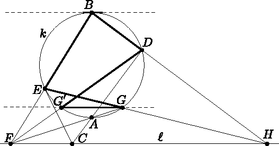
 

 
6. ábra
 

 
III. megoldás. Definiáljunk a k kör pontjain egy kétváltozós műveletet, amelyet az összeadáshoz hasonlóan a + jellel fogunk jelölni, a következőképpen. Válasszunk ki egy tetszőleges, ℓ-re nem illeszkedő O pontot a körön. A kör bármely X, Y pontpárjára szerkesszük meg ℓ és az XY egyenes metszéspontját. (Ha X=Y, akkor az XY egyenes az érintő. Ha a két egyenes párhuzamos, akkor a metszéspont ℓ ideális pontja.) A metszéspontot kössük össze O-val, és szerkesszük meg az egyenes és a kör másik metszéspontját. (Ha az egyenes érinti a kört, akkor a másik metszéspont is O.) Ez a pont legyen X+Y (7. ábra).
 

 
7. ábra
 

A + művelet a definíció alapján biztosan kommutatív, X+Y=Y+X. Az is igaz, hogy asszociatív, azaz (X+Y)+Z=X+(Y+Z) tetszőleges X, Y, Z pontok esetén. Ez a tulajdonság ekvivalens a Pascal-tétellel (8. ábra)
 

 
8. ábra
 

Ezen kívül könnyen ellenőrizhető, hogy tetszőleges X pontra X+O=X, és létezik olyan Y pont, amelyre X+Y=O. (Ezt a pontot mostantól jelölhetjük (-X)-szel is.) Összefoglalva, a kör pontjai ezzel a + művelettel egy kommutatív csoportot alkotnak, amelynek neutrális eleme az O pont.
Térjünk most rá a feladat állításának bizonyítására. Legyen O=A, és jelöljük H-val a DF egyenes és k második metszéspontját. Azt akarjuk megmutatni, hogy GH párhuzamos az ℓ egyenessel, ami azt jelenti, hogy G+H=O (9. ábra).
 

 
9. ábra
 

 

 
10. ábra
 

Az ábráról jól leolvasható, hogy B+B=O, E+E=D és B+E=D+H=G. Ezekből
G+H=(B+E)+(B+E-D)=(B+B)+(E+E-D)=O+O=O.

 
Megjegyzések. 1. A felhasznált + műveletet az algebrai geometriából, a harmadfokú görbék elméletéből vettük át. Ha γ egy harmadfokú síkgörbe (amelyet tehát egy kétváltozós harmadfokú egyenlet ír le), és O a γ egy tetszőleges pontja, akkor a görbe pontjain a feladatban leírt módon értelmezhetünk egyfajta összeadást (10. ábra). Ezzel a művelettel a görbe pontjai mindig kommutatív csoportot alkotnak.
A megoldásban azt az elfajuló esetet alkalmaztuk, amikor γ a k kör és az ℓ egyenes uniója. A + művelet ebben az esetben is értelmezhető a teljes görbén, bár két ℓ-en fekvő pont összegét máshogy kell definiálni. A megoldáshoz csak k pontjaira volt szükségünk, amelyek a teljes csoportnak egy részcsoportját alkotják.
2. A pontok közötti összefüggésekből több más geometriai tény is könnyen levezethető. Például könnyen ellenőrizhető, hogy G+G=E+E, B+G=E és B+D=G+E. Ezek geometriai állításokra lefordítva azt mondják, hogy CG is érinti a kört, továbbá a BG és AE, illetve BD és GE egyenesek metszéspontja is ℓ-re esik. (Ezeket a pontokat is feltüntettük a 9. ábrán.)
 
A dolgozatok tanulságai
 

A legtöbb versenyző az I. megoldáshoz hasonló elemi úton a szögek összeszámolásával és a kerületi szögek tételének többszöri alkalmazásával ‐ de előjeles szögek használata nélkül ‐ oldotta meg a feladatot. Ezen a dolgozatoknak nagy részében a diszkusszió részben vagy teljesen hiányzott. A teljes megoldáshoz az ábrának és a pontok elhelyezkedésének legalább 4-féle változatát kellett volna megkülönböztetni, ezt egyedül Bogár Péter tette meg. Azok, akiknél a diszkusszió teljesen hiányzott, és a megoldást csak az ábra egyféle elrendezésére számolták végig, 3 pontot kaptak.