Kezdőlap


Feladat:	B.3854	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Cséke Balázs
Füzet:	2006/szeptember, 342 - 343. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Alakzatok hasonlósága, Háromszögek nevezetes tételei, Feladat
Hivatkozás(ok):	Feladatok: 2005/november: B.3854

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyenek a háromszög oldalai $a \leq b \leq c$ , a megfelelő súlyvonalak pedig $s_{a}$ , $s_{b}$ , $s_{c}$ . A súlyvonalak négyzetére vonatkozó jól ismert összefüggés szerint

\begin{matrix} 4 s_{a}^{2} = 2 c^{2} + 2 b^{2} - a^{2}, 4 s_{b}^{2} = 2 c^{2} + 2 a^{2} - b^{2} és 4 s_{c}^{2} = 2 a^{2} + 2 b^{2} - c^{2} \end{matrix}

(ezek könnyen levezethetők abból, hogy bármely paralelogramma oldalainak négyzetösszege megegyezik átlóinak négyzetösszegével, ld. 1. ábra). Látható, hogy

s_{a} \geq s_{b} \geq s_{c}

. Mivel két háromszög pontosan akkor hasonló, ha megfelelő oldalaik négyzeteinek aránya megegyezik, azért a követelmény teljesülésének szükséges és elégséges feltétele

\begin{matrix} \frac{2 c^{2} + 2 b^{2} - a^{2}}{c^{2}} = \frac{2 c^{2} + 2 a^{2} - b^{2}}{b^{2}} = \frac{2 a^{2} + 2 b^{2} - c^{2}}{a^{2}} . \end{matrix}

(1)

1. ábra

Ezekből az egyenletekből rendezéssel kapjuk, hogy a

\begin{matrix} 2 b^{2} c^{2} + 2 b^{4} - a^{2} b^{2} = 2 c^{4} + 2 a^{2} c^{2} - b^{2} c^{2} és a 2 a^{2} c^{2} + 2 a^{4} - a^{2} b^{2} = 2 a^{2} b^{2} + 2 b^{4} - b^{2} c^{2} \end{matrix}

egyenlőségeknek egyszerre kell teljesülniük. A két egyenletet összeadva, rendezés után a

\begin{matrix} 0 = a^{4} + 2 b^{2} c^{2} - c^{4} - 2 a^{2} b^{2} = (a^{2} - c^{2}) (a^{2} + c^{2} - 2 b^{2}) \end{matrix}

egyenlethez jutunk. Ha

a^{2} = c^{2}

, akkor

a = c

, amit az első egyenletbe visszaírva kapjuk, hogy

b = c

, azaz ebben az esetben a háromszög szabályos. Ha

a^{2} + c^{2} - 2 b^{2} = 0

, vagyis

a^{2} + c^{2} = 2 b^{2}

(ami mellesleg szabályos háromszög esetén is igaz), akkor mindkét (1)-beli egyenlőség fennáll, mert

\begin{matrix} \frac{2 c^{2} + (a^{2} + c^{2}) - a^{2}}{c^{2}} = \frac{2 c^{2} + 2 a^{2} - \frac{a^{2} + c^{2}}{2}}{\frac{a^{2} + c^{2}}{2}} = \frac{2 a^{2} + (a^{2} + c^{2}) - c^{2}}{a^{2}} = 3. \end{matrix}

Tehát egy háromszög súlyvonalaiból pontosan akkor szerkeszthető hozzá hasonló háromszög, ha a háromszög valamely két oldalának négyzetösszege megegyezik a harmadik oldal négyzetének kétszeresével. Ez a feltétel a szabályos háromszögön kívül teljesül például abban a derékszögű háromszögben, amelynek oldalai 2,

2 \sqrt[]{2}

és

2 \sqrt[]{3}

(súlyvonalai pedig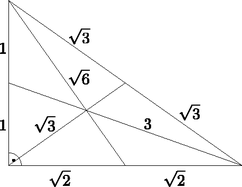

\sqrt[]{3}

\sqrt[]{6}

és 3).

2. ábra