Kezdőlap


Feladat:	C.828	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Buza Dániel István
Füzet:	2006/szeptember, 334 - 335. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Terület, felszín, C gyakorlat
Hivatkozás(ok):	Feladatok: 2005/november: C.828

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelöljük 2005-öt $a$ -val, 2006-ot $b$ -vel. Ekkor az egyenletek:

\begin{matrix} y = - x + a, & (1) \\ \frac{x}{a} + \frac{y}{b} = 1, & (2) \\ \frac{x}{b} + \frac{y}{a} = 1. & (3) \end{matrix}

Számítsuk ki az egyenesek metszéspontjainak koordinátáit.
Az (1) és (2) egyenletből:

\begin{matrix} \frac{x}{a} + \frac{- x + a}{b} = 1, innen \\ b x - a x + a^{2} = a b, \\ x (b - a) = a b - a^{2}, \\ x = \frac{a (b - a)}{b - a} = a és y = 0. \end{matrix}

P_{1} (a; 0)

a két egyenes metszéspontja.
Az (1) és (3) egyenesek metszéspontja legyen

P_{2}

. Az egyenletek szimmetriájából következik, hogy

P_{2} (0; a)

.
A (2) és (3) egyenesek

P_{3}

metszéspontjának koordinátáit megkapjuk, ha az egyenletrendszert megoldjuk. A (2) egyenletből:

x = \frac{a b - a y}{b}

. Helyettesítsük ezt (3)-ba:

\begin{matrix} \frac{a b - a y}{b^{2}} + \frac{y}{a} = 1, \\ a^{2} b - a^{2} y + y b^{2} = a b^{2}, és innen y = \frac{a b}{a + b} . \end{matrix}

Az egyenletek szimmetriája miatt

P_{3}

x

koordinátája ugyanennyi, azaz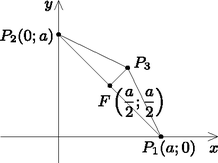

\begin{matrix} P_{3} (\frac{a b}{a + b}; \frac{a b}{a + b}) . \end{matrix}

P_{1} P_{2} P_{3}

háromszög területét kell meghatározni.

Könnyű belátni, hogy a

P_{1} P_{2} P_{3}

háromszög egyenlő szárú. Alapja

\bar{P_{1} P_{2}}

, az ehhez tartozó magassága

P_{3}

-ból indul és felezi a

P_{1} P_{2}

szakaszt.

P_{1} P_{2}

felezőpontja

F

, koordinátái

(\frac{a}{2}; \frac{a}{2})

\begin{matrix} \bar{P_{1} P_{2}} = a \sqrt[]{2}, \bar{P_{3} F} = \sqrt[]{2 {(\frac{a b}{a + b} - \frac{a}{2})}^{2}} = (\frac{a b}{a + b} - \frac{a}{2}) \sqrt[]{2} . \end{matrix}

A terület:

\begin{matrix} T = \frac{a \sqrt[]{2}}{2} \cdot \frac{a (b - a)}{2 (a + b)} \cdot \sqrt[]{2} = \frac{a^{2} (b - a)}{2 (a + b)} . \end{matrix}

Írjuk be

a

és

b

számértékeit, kapjuk, hogy

\begin{matrix} T = \frac{2005^{2}}{2 (2005 + 2006)} \approx 501, 13 területegység. \end{matrix}