Kezdőlap


Feladat:	113. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baligovics G. , Böszörményi Gy. , Deutsch T. , Elek T. , Fischer Gy. , Fischer Rózsi , Fürst L. , Gregor A. , Grünhut P. , Hajós Gy. , Horváth K. , Keil M. , Klein Eszter , Kronich Erzsébet , Latzer Magda , Lukács E. , Mischung Ilona , Németh B. , Neufeld B. , Policsek L. , Rácz E. , Ság M. , Schlüssler E. , Sveiczer M. , Terebesi P. , Vasváry L. , Weisz F. , Wolf M. , Wolkóber L. , Ziegler Imre , Zólomy I.
Füzet:	1927/április, 252 - 253. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Lejtő, Erőrendszer eredője
Hivatkozás(ok):	Feladatok: 1927/február: 113. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A lejlőre elhelyezett testre 4 erő hat; az egyensúlynak első feltétele, hogy e négy erőnek a lejtő irányába eső összetevőinek algebrai összege zérus legyen, tehát ha $x$ a lejtő hajlásszöge:

\begin{matrix} Q sin x - \frac{Q}{3} sin x - \frac{Q}{3} - \frac{Q}{3} cos x = 0 \\ 2 sin x - (1 + cos x) = 0, vagy 4 sin \frac{x}{2} cos \frac{x}{2} - 2 c o s^{2} \frac{x}{2} = 0. \end{matrix}

Kizárva a

cos \frac{x}{2} = 0,

azaz

x = π

esetet (amidőn nincs lejtő),

\begin{matrix} tg \frac{x}{2} = \frac{1}{2}; x = 2 arc tg \frac{1}{2} = 53^{\circ} 7' 48'' . \end{matrix}

Az egyensúly második feltétele, hogy az erők eredője a lejtőre merőleges és a lejtő síkja felé legyen irányítva.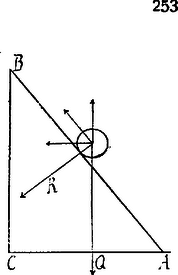

Az erőknek a lejtőre merőleges összetevőinek összege :

\begin{matrix} R = Q cos x - \frac{Q}{3} cos x + \frac{Q}{3} sin x = \frac{Q}{3} (2 cos x + sin x) = \\ = \frac{Q}{3} [2 \frac{1 - {tg}^{2} \frac{x}{2}}{1 + {tg}^{2} \frac{x}{2}} + \frac{tg - \frac{x}{2}}{1 + {tg}^{2} \frac{x}{2}}] = \frac{2 Q}{3} \end{matrix}

tekintettel arra, hogy

tg \frac{x}{2} = \frac{1}{2} .

R

előjelre megegyezik

Q cos x

előjelével.

Ziegler Imre (szombathelyi áll. főreál VII. o.)