Kezdőlap


Feladat:	12. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bayer István , Benedek V. , Körtvélyesi F. , Macz F. , Medgyesi Ö. , Séra I. , Wessel I.
Füzet:	1925/május, 97. oldal		PDF \| MathML
Témakör(ök):	Feladat
Hivatkozás(ok):	Feladatok: 1925/március: 12. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . A rúd egyensúlyban van, ha súlypontja $O$ ponton átmenő függélyesbe esik.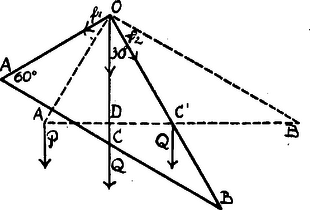
Az $A O B Δ$ derékszögű $O$ -nál, mert $1^{2} + {(\sqrt[]{3})}^{2} = 2^{2}$ . Hegyesszöge $30^{\circ}$ , ill. $60^{\circ}$ . Az $A B$ rúd súlypontja $C$ , az $A B$ felezőpontja. $O C = A C = O A = 1 m$ . Egyensúly esetén $O A$ a vízszintessel $30^{\circ}$ -ú szöget zár be.

2^{\circ}

. Ha a rúd súlyának támadó pontját

O

-ba helyezzük, ezt az erőt két összetevőre bontjuk

O A

ill.

O B

irányban.

\begin{matrix} O A & irányában & f_{1} = 10 \cdot cos 60^{\circ} = \frac{10}{2} = 5 kg \\ O B & ,, & f_{2} = 10 \cdot cos 30^{\circ} = \frac{10 \sqrt[]{3}}{2} = 5 \sqrt[]{3} = 8, 66 kg \end{matrix}

3^{\circ}

. Ha azt akarjuk, hogy a rúd vízszintes helyzetbe kerüljön,

P

súlynak és a rúd súlyának

O

pontra vonatkozólag egyenlő forgató nyomatékkal kell bírnia. Ha a rúd vízszintes helyzetben van,

C

pont

C'

-be kerül és az

O

ponton átmenő függélyes

A C'

-t felezi, mert

A O C' Δ

egyenlő oldalú. Tehát, hogy a vízszintes egyensúlyi helyzet létrejöjjön, kell, hogy

P \cdot A D = 10 \cdot C' D

legyen; mivel pedig

A D = C' D

P = 10 kg

Bayer István (kir. kath. rg. VII. o. Mezőkövesd)