Kezdőlap


Feladat:	139. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berényi F. , Bucsy I. , Glatz L. , Klein Eszter , Klein M. , Kozma A. , Lemberger Klára , Molnár László , Neufeld B. , Pollák A. , Rónai Gy. , Rosenthal E. , Schächter I. , Somogyi L. , Stern D. , Strasser P. , Weisz Lili , Wolf M.
Füzet:	1927/november, 89 - 90. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Fényinterferencia
Hivatkozás(ok):	Feladatok: 1927/szeptember: 139. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Legyen $A B = 0, 1 cm =a$ , $O C = 200 cm = d$ és $C D = σ$ . Az $A$ és $B$ résekből kiinduló fénysugarak útkülönbsége a $d$ távolságra levő ernyő $D$ pontjában: $A D = B D = A H$ , ha $H$ a $B$ vetülete az $A 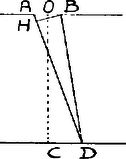D$ -n.

Eszerint

\begin{matrix} σ = C D = O C tg C O D ≅ d \cdot C O D azaz C O D = \frac{σ}{d}, \end{matrix}

ha t. i. a kis

C O D

szög tangense helyett a

C O D

szög mérőszámát vesszük.

\begin{matrix} A H = A B \cdot sin A B H = A B \cdot sin C O D ≅ a \cdot C O D = a \cdot \frac{σ}{d} . \end{matrix}

D

C

-hez legközelebbi fényes csík, az

A H

útkülönbség a fény

λ

hullámhosszával egyenlő. tehát

\begin{matrix} λ = \frac{a σ}{d} = \frac{0, 1 \times 0, 12}{200} cm = 6 \cdot 10^{- 5} cm = 0, 6 μ . \end{matrix}

2^{\circ}

. Jelentse

τ

az időt, amely alatt a fénysugár ez

e = 0, 03 cm

. vastagságú csillámlemezen áthalad, továbbá

v

a fénysebességet a levegőben,

v'

a csillámlemezben;

\frac{v}{v'} = n = 1, 5

. Minthogy

v' τ = e

τ = \frac{e}{v'}

és így a csillámlemez által okozott útkülönbség

\begin{matrix} δ \cdot v τ - v' τ = (v - v') τ = (v - v') \frac{e}{v'} = (\frac{v}{v'} - 1) e = (n - 1) e \end{matrix}

\begin{matrix} δ = 0, 03 \cdot (1, 5 - 1) = 0, 015 cm. \end{matrix}

Ezen

δ

útkülönbség folytán a középső csík eltolódása

σ = \frac{d δ}{a}

. (Ha t. i. a fenti

A H = \frac{a σ}{d}

összefüggést

σ

-ra megoldjuk és

A H = δ

útkülönbség). A numerikus értékeket helyettesítve

\begin{matrix} σ = \frac{200 \times 0, 015}{0, 1} = 30 cm . \end{matrix}

Molnár László (Kölcsey Ferenc rg. VIII. o. Bp. VI.)