Kezdőlap


Feladat:	231. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Góber J. , Hajós György , Hapka I. , Ignátz P. , Mattyasovszky L. , Papp Gy. , Pomóthy D. , Stern M. , Straubert Jenő
Füzet:	1929/szeptember, 29. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Merev test egyensúlya
Hivatkozás(ok):	Feladatok: 1929/április: 231. fizika feladat

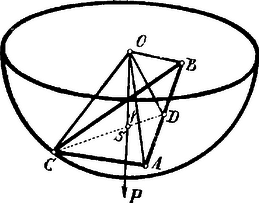
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C$ egyenlőszárú háromszög $C$ csúcsánál fekvő szög legyen derékszög; súlypontja $S$ a $C D$ oldalfelezőn fekszik, mely merőleges az $A B$ átfogóra.^{$^{*}$} $O$ a gömb középpontja, $P$ a lemez súlya.

A lemezre az

A

B

C

pontokban a gömb reakciója hat

A O

B O

C O

irányban (a gömbfelületre merőlegesen!). Ezen három erő eredője egyensúly esetén

P

-vel egy egyenesben, vele egyenlő és ellenkező irányú tartozik lenni. Ebből következik, hogy az

S

pont az

O

ponton áthaladó függőlegesben helyezkedik el, továbbá, hogy az

O C D

sík is függőleges. Az

A B

átfogó vízszintes, mert az

O D

és

C D

egyenesekre, tehát az

O C D

síkra merőleges: az

O D

pedig merőleges az

A B C

síkra, mert az

O

és

D

pontok mindegyike egyenlő távolságban van az

A

B

C

pontoktól. Eszerint azon szög, melyet

O S

alkot

S D

-vel, a keresett hajlásszög:

q

és

O S

a kiszámítandó távolság. Az

O S D

derékszögű háromszögből ^{$^{*}$}

\begin{matrix} tg φ = \frac{O D}{S D} és {\bar{O S}}^{2} = {\bar{O D}}^{2} + {\bar{S D}}^{2} . \end{matrix}

Azonban:

\begin{matrix} S D = \frac{C D}{3}; C D = \frac{a \sqrt[]{2}}{2}; \\ {\bar{O D}}^{2} = {\bar{A O}}^{2} - {\bar{A D}}^{2} = r^{2} - \frac{a^{2}}{2} . \end{matrix}

Helyettesítve ezeket

\begin{matrix} tg φ = \frac{3}{a} \sqrt[]{2 r^{2} - a^{2}} és O S = \frac{1}{3} \sqrt[]{9 r^{2} - 4 a^{2}} . \end{matrix}

Az egyensúlyi helyzet feltétele, hogy

\begin{matrix} a = r \sqrt[]{2} . \end{matrix}

a = r \sqrt[]{2}

, akkor

φ = 0

és ^{$^{*}$}

O S = \frac{r}{3}

Straubert Jenő (Baross Gábor reál VII. o. Szeged.)

^{$^{*}$}

A B = B D = C D

^{$^{*}$}A derékszög B-nél!

^{$^{*}$}Az $A B C$ sík függőleges helyzetű, az $A B$ átfogó a gömb $O$ középpontján megy át vízszintes helyzetben ( $A B - 2 r)$ - Az $o s = \frac{r}{3}$ érték minimum!