| Feladat: | 209. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Aczél I. , Balogh K. , Bátorffy V. , Brünn R. , Detrich B. , Erdélyi L. , Erdős Pál , Etre S. , Fenyves F. , Góber J. , Hajós György , Ignátz P. , Jacobi A. , Jónás P. , Katz D. , Kelemen Sz. , Kohn P. , Lindtner P. , Mattyasovszky L. , Papp Gy. , Papp L. , Pomóthy D. , Schwarz E. , Sebestyén J. , Sebők Imre , Soldinger J. , Székely Gy. , Székely Lilly , Szolovits D. , Sztruhár A. , Walient P. | ||
| Füzet: | 1929/február, 165 - 166. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Gömbtükör, Síktükör | ||
| Hivatkozás(ok): | Feladatok: 1928/december: 209. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen a gömbtükör optikai, a geometriai középpontja és a gyújtópontja; pontban metszi a sík üveglap a gömbtükör főtengelyét. A pontszerű fényforrás nem lehet az és között, mert ekkor a gömbtükör virtuális képet hoz létre a tükör mögött. Ha a fényforrás -ben van, és között, akkor a gömbtükör által létesített valódi kép pontban van, ahol a síktükör is képet (virtuális) hoz létre; ha pedig a fényforrás -ban van, akkor a gömbtükör által létesített valódi képe -ben van és ugyanitt hoz létre a síktükör is (virtuális) képet. A feladatnak eszerint két megoldása van. 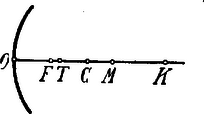 Legyen , ; akkor
és gyökei tehát az Feladatunkban foglalt adat kielégíti ezen feltételt és így a feladat megoldható. A megadott numerikus értékeket helyettesítve Ezen gyökök mindegyike oly távolságot határoz, amely a feladat követelményeinek megfelel.
|