Kezdőlap


Feladat:	271. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baranyai K. , Déry E. , Fejér Gy. , Gohn E. , Jakobovits L. , Kauders Éva , Klein T. , Kmoschek P. , Kövesdi Dezső , Nay A. , Papp Gy. , Raisz I. , Simon Á. , Singer Gy. , Stern M. , Straubert J. , Szidarovszky J. , Vincze I.
Füzet:	1930/április, 255 - 256. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Mozgócsiga, Merev test egyensúlya, Állócsiga
Hivatkozás(ok):	Feladatok: 1930/február: 271. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fonál minden pontján ugyanakkora $T$ tenziós erő hat.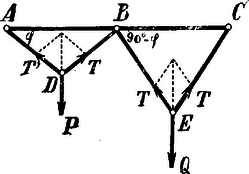

Egyensúly esetén

\begin{matrix} P = 2 T sin φ, & (1) \\ Q = 2 T cos φ . & (2) \end{matrix}

Másrészt, mivel

D B + B E = l

\begin{matrix} \frac{d}{cos φ} + \frac{d}{sin φ} = l, vagyis d (sin φ + cos φ) = l sin φ cos φ . \end{matrix}

(3)

A (3) megoldása céljából emeljünk négyzetre mindkét oldalon:

\begin{matrix} d^{2} (sin^{2} φ + cos^{2} φ + 2 sin φ cos φ) = l^{2} {(sin φ cos φ)}^{2} \\ d^{2} (1 + sin 2 φ) = \frac{l^{2}}{4} {sin}^{2} 2 φ azaz sin^{2} 2 φ - \frac{4 d^{2}}{l^{2}} sin 2 φ - \frac{4 d^{2}}{l^{2}} = 0. & (4) \end{matrix}

A (4) egyenletnek két ellenkező előjelű valós gyöke van. Minthogy

0 < φ < 90^{\circ}

, azért

0 < 2 φ < 180^{\circ}

, tehát

0 < sin 2 φ \leq 1

. Eszerint a (4)-nek csak a pozitív gyöke felel meg, ez is csak akkor, ha

1

-nél nem nagyobb. Ha

sin 2 φ = 0

, akkor a (4) baloldala:

f (0) = - \frac{4 d^{2}}{l^{2}} < 0

.
Kell tehát, hogy

\begin{matrix} f (1) = 1 - \frac{8 d^{2}}{l^{2}} \geq legyen, azaz : \frac{l}{d} ≧ 2 \sqrt[]{2} . \end{matrix}

Ez a feltétele annak, hogy a szóban forgó egyensúlyi helyzet létrejöhessen és ekkor (1)-ből és (2)-ből:

\frac{P}{Q} = tg φ

Kövesdi Dezső (Somssich Pál rg. VII. o. Kaposvár)