|
| Feladat: |
253. fizika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Albrecht J. , Aschenbrier E. , Barna I. , Barok Gy. , Barta F. , Barta I. , Beke I. , Budó Ágoston , Csernák J. , Csíky J. , Déman P. , Dénes P. , Déry E. , Erdélyi Erzsi , Ereky V. , Fejér Gy. , Feldheim E. , Gerber Edit , Glasner Mária , Gohn E. , Hadel M. , Jánky Mária , Jánosi S. , Kardos F. , Kiss Gy. , Klein Béla , Klein T. , Kmoschek P. , Kövesdi D. , Ligeti M. , Molnár Ernő , Molnár J. , Nagymihály L. , Nay A. , Németh J. , Papp Gy. , Perneczky B. , Pomóthy D. , Radó Gy. , Radványi M. , Richter I. , Salamin J. , Schossberger A. , Sebők Gy. , Simon Á. , Singer Gy. , Stern M. , Straubert J. , Szabó Piroska , Szebasztián Rózsa , Sztranszky M. , Varga T. , Vas Gy. , Vincze I. , Weisz F. , Zsemlye B. |
| Füzet: |
1930/január,
157 - 158. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Feladat, Pontrendszerek mozgásegyenletei, Egyenletesen változó mozgás (Változó mozgás), Egyenesvonalú mozgás lejtőn |
| Hivatkozás(ok): | Feladatok: 1929/november: 253. fizika feladat |
|
|
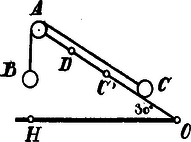
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. . Az tömegű testet a hajlásszögű lejtőn erő mozgatja az felé.
Az tömegű testre ható nehézségi erő ; az egész rendszerre ható erő és ez gyorsulást létesít. Ezen gyorsulással a test 1 m utat tesz meg 2 sec. alatt, azaz | |
Minthogy , és .
. Amikor a test -ba ér, a test a lejtőn 1 m utat tett meg, ugyancsak gyorsulással, tehát sebessége . Másrészt: , tehát és . Ha tehát ekkor a test -be jutott a lejtőn, kezdősebességgel mozog az erő ellenében; eleven erejét felemészti ezen erő ellenében végzett munka, amíg -be jut, azaz
. Amidőn a test a -ből visszatér -ba, gyorsulása a lejtőn: . Így az pontba | |
sebességgel jut vissza.
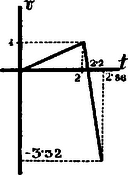
Amint láttuk, akkor amikor a a -ba jutott, sebessége és így a sebessége is a -ben . A sebesség tehát -tól -ig egyenletesen növekedett: függvénynek megfelelőleg. Ennek grafikonja a pontból a pontig emelkedő egyenes.
Ezen ponttól, a sebesség csökken, t. i. a gyorsulás , azaz Ezen függvénynek leszálló egyenes felel meg. | |
Az pontban a sebesség, irányára való tekintettel ‐ ;
tehát az egyenletből .
| Klein Béla (Kölcsey Ferenc rg. VII. o. Bp. VI.) |
|
|
 PDF
PDF