Kezdőlap


Feladat:	244. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balassa J. , Barok Gy. , Budó Ágoston , Déman P. , Déry E. , Faragó T. , Fekete F. , Grünwald T. , Kauders Éva , Kiss Gy. , Klein B. , Klein T. , Kövesdi D. , Ligeti M. , Molnár J. , Perneczky Béla , Schossberger A. , Straubert J. , Vági L. , Varga T. , Vincze I.
Füzet:	1929/november, 94 - 95. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Vektorok
Hivatkozás(ok):	Feladatok: 1929/szeptember: 244. fizika feladat

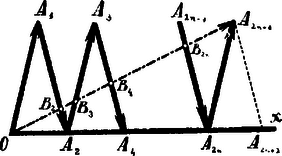
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Itt avval az egyszerű esettel állunk szemben, amidőn a vektorok mindegyike a megelőző végpontjából indul ki. Eredőjük az első kezdőpontját az utolsó végpontjával köti össze, azaz ${\vec{O A}}_{2 n + 1}$ .

2^{\circ}

. Legyen

O A_{1} = A_{1} A_{2} = \dots = A_{2 n} A_{2 n + 1} = a

. Az eredő

{\vec{O A}}_{2 n + 1}

A_{1} A_{2}

-t

B_{2}

, az

A_{2} A_{3}

-t

B_{3}, ...

A_{2 n + 1} A_{2 n}

-t

B_{2 n}

pontban metszi. A háromszögek hasonlóságából következik:

\begin{matrix} \begin{matrix} A_{2} B_{2} & = \frac{a}{n + 1}, & A_{2} B_{3} & = \frac{a}{n}, \\ A_{4} B_{4} & = \frac{2 a}{n + 1}, & A_{4} B_{5} & = \frac{2 a}{n}, \\ \dots \\ A_{2 n} B_{2 n} & = \frac{n a}{n + 1}, & A_{2 n - 2} B_{2 n - 1} & = \frac{(n - 1) a}{n} . \end{matrix} \end{matrix}

Perneczky Béla (premontrei rg. VIII. o. Szombathely)