Kezdőlap


Feladat:	C.818	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	2006/március, 147 - 148. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Körök, Négyzetek, Terület, felszín, C gyakorlat
Hivatkozás(ok):	Feladatok: 2005/szeptember: C.818

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelöljük a kör sugarát $r$ -rel, a négyzet oldalát $a$ -val. A kerületek egyenlőségéből: $2 r π = 4 a$ , következik, hogy $r = \frac{2 a}{π}$ . A négyzet egyik csúcsát jelölje $A$ , a közös középpontot $O$ , ekkor $\bar{A O} = \frac{a \sqrt[]{2}}{2}$ . Állítjuk, hogy

\begin{matrix} \frac{a \sqrt[]{2}}{2} > r, \end{matrix}

(1)

tehát a négyzetnek van pontja a körön kívül. Helyettesítsük

r

előbb kapott értékét (1)-be:

\begin{matrix} \frac{a \sqrt[]{2}}{2} > \frac{2 a}{π}, \end{matrix}

innen

a

-val egyszerűsítve és rendezve kapjuk, hogy

π > 2 \sqrt[]{2} (\approx 2, 8284)

. Az egyenlőtlenség valóban fennáll. A négyzet alakú terítő a körből 4 darab egybevágó körszeletet nem fed le.
Messe a kör a négyzet egy oldalát az

M_{1}

M_{2}

pontokban (lásd az ábrát),

O

-ból az

M_{1} M_{2}

-re állított merőleges talppontját jelölje

P

, a

P O M_{1}

szöget

\frac{α}{2}

. Az

O M_{1} M_{2}

körszelet területét megkapjuk, ha az

O M_{1} M_{2}

körcikk területéből kivonjuk az

O M_{1} M_{2}

háromszög területét.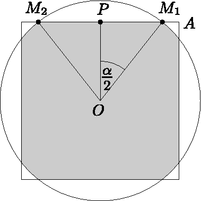

Ehhez először az

\frac{α}{2}

szöget határozzuk meg. A

P O M_{1}

háromszögből

P O = \frac{a}{2}

O M_{1} = r = \frac{2 a}{π}

és

\begin{matrix} cos \frac{α}{2} = \frac{O P}{O M_{1}} = \frac{\frac{a}{2}}{\frac{2 a}{π}} = \frac{π}{4}, \end{matrix}

innen

\frac{α}{2} \approx 38, 24^{\circ}

α \approx 76, 48^{\circ}

és

sin α \approx 0, 9723

.
Az

O M_{1} M_{2}

körcikk területe:

t_{1} = \frac{π α r^{2}}{360^{\circ}}

, az

O M_{1} M_{2}

háromszög területe:

t_{2} = \frac{r^{2} sin α}{2}

. A körszelet területe:

\begin{matrix} t_{1} - t_{2} \approx r^{2} (0, 6674 - 0, 4862) = r^{2} \cdot 0, 1812. \end{matrix}

A négy körszelet együttes területe:

0, 7248 r^{2}

. A négyzet alakú terítő által lefedett terület:

\begin{matrix} r^{2} π - 0, 7248 r^{2} \approx 2, 4168 r^{2} . \end{matrix}

Az asztallap területe egyenlő a kör területével:

r^{2} π

. A két terület hányadosa

\approx \frac{2, 4168}{π} \approx 0, 7693

. A terítő az asztallap területének körülbelül a 77%-át takarja.