Kezdőlap


Feladat:	547. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Farkas Imre , Schwarz János
Füzet:	1936/február, 181 - 183. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fizika, Egyéb kényszermozgás
Hivatkozás(ok):	Feladatok: 1935/december: 547. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

b) A lengési idő tárgyalásánál szintén a fenti képpel élhetünk s a két testet összekötő rugó tömegét elhanyagoljuk.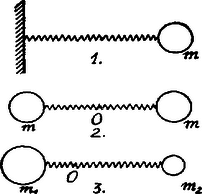
Ha az óra a zsebünkben van vagy az asztalon fekszik, szóval, ha az óratest nem mozoghat, akkor azzal az esettel van dolgunk, midőn a rugó egyik vége mereven meg van erősítve, vagyis egy, az $m$ tömegű testhez képest végtelen nagy tömegű testhez van kötve. (l. 1. ábra).

Ezen eset tárgyalása általánosan ismert. Ha

a

azon erő, amely a rugót 1 cm-rel meghosszabbítja, akkor a rezgési idő

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{a}} . \end{matrix}

(4)

Vegyük most azon esetet, midőn a rugó mindkét végére egy‐egy

m

tömegű test van erősítve. A két test ez esetben nyilván úgy fog mozogni, hogy a mozgásuk fázisa mindig ellentett (l. 2. ábra), az amplitúdójuk pedig egyenlő, úgy, hogy a tömegközéppontjuk,

O

, ami a rugó közepére esik, nyugalomban marad. De akkor a rugónak ezt a pontját akár rögzíthetjük is s akkor rögtön belátjuk, hogy a két test úgy fog rezegni, mintha fele olyan hosszú rugó hatna reájuk.
Miután azonban ugyanazon rugónak a fele kétszer olyan ,,erős'', azaz ugyanakkora megnyújtáshoz kétszer akkora erő kell, most

a

helyébe

2 a

teendő és a lengési idő

\begin{matrix} T' = 2 π \sqrt[]{\frac{m}{2 a}} = T \sqrt[]{\frac{1}{2}} \end{matrix}

(5)

lesz, azaz a testek

\sqrt[]{2} = 1, 41

-szer gyorsabban fognak rezegni.
Általában, ha a két test tömege

m_{1}

és

m_{2}

, a tömegközéppont, azaz a testnek nyugalomban maradó

O

pontja, a két (pontszerűnek képzelt) testtől olyan távolságban van, hogy (l. 3. ábra)

\begin{matrix} \frac{O M_{1}}{O M_{2}} = \frac{m_{2}}{m_{1}} . \end{matrix}

(6)

Tekintsük pl. az

m_{2}

test mozgását. Legyen a rugó hossza

l

; akkor, amíg

m_{1} = \infty

m_{2}

lengésideje

\begin{matrix} T_{2} = 2 π \sqrt[]{\frac{m_{2}}{a}} . \end{matrix}

(4a)

m_{1}

véges, akkor a fentiek szerint az

m_{2}

úgy rezeg, mintha a rugó hossza kisebb lenne, t. i.

\begin{matrix} O M_{2} = l' = \frac{m_{1}}{m_{1} + m_{2}}, \end{matrix}

az 1 cm megnyújtáshoz szükséges erő pedig

\begin{matrix} a' = a : \frac{m_{1}}{m_{1} + m_{2}} = a \frac{m_{1} + m_{2}}{m_{1}} . \end{matrix}

A megváltozott lengési idő tehát:

\begin{matrix} T'_{2} = 2 π \sqrt[]{\frac{m_{2}}{a} \cdot \frac{m_{1}}{m_{1} + m_{2}}} = T_{2} \sqrt[]{\frac{m_{1}}{m_{1} + m_{2}}} . \end{matrix}

Ugyanezen képlet alkalmazható a mi esetünkre is, csupán a tömegek helyett a tétlenségi nyomatékokat kell tennünk.
Az eredmény tehát az, hogy az órát a feltüntetett módon felfüggesztve, az óra sietni fog, ugyanis a lengés ideje

\begin{matrix} \sqrt[]{\frac{K_{1}}{K_{1} + K_{2}}} -szerese annak, ami volt. \end{matrix}

Dr. Selényi Pál.

Az 547. feladatban felvetett kérdésre, habár nem kimerítően, de elég jól válaszoltak: Farkas Imre és Schwarz János (Szent László rg. VII. a. o. Bp.)