Kezdőlap


Feladat:	606. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Blahó Miklós , Krisztonosich Jenő , Pálos Peregrin , Than Károly , Vajda József , Weisz Alfréd
Füzet:	1937/május, 289 - 290. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Feladat
Hivatkozás(ok):	Feladatok: 1937/március: 606. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az elhajított súlygolyó mozgását az

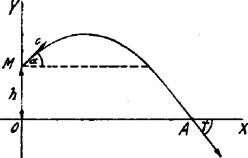
\begin{matrix} x = c cos α \cdot t, y = c sin α \cdot t - \frac{1}{2} g t^{2} + h \end{matrix}

egyenletek írják le, ha a derékszögű koordinátarendszert szokásos módon vesszük fel és kezdőpontja az

O

pont.

A mozgó pont pályájának egyenlete

\begin{matrix} y = tg α \cdot x - \frac{1}{2} \frac{g}{c^{2} cos^{2} α} x^{2} + h . \end{matrix}

a) Az

A

pontra nézve

y = 0

; az

O A

távolság az

\begin{matrix} x tg α - \frac{1}{2} \frac{g}{c^{2} cos^{2} α} x^{2} + h = 0, ill. a g x^{2} - c^{2} sin 2 α \cdot x - 2 h c^{2} cos^{2} α = 0 ... \end{matrix}

(1)

egyenletnek gyöke. Ezen egyenletnek mindig valós és ellenkező előjelű gyökei vannak; közülük csak a pozitív felel meg feladatunknak és így

\begin{matrix} O A = x = \frac{1}{2 g} (c^{2} sin 2 α + \sqrt[]{c^{4} sin^{2} 2 α + 8 g h c^{2} cos^{2} α)} = \\ = \frac{c cos α}{g} (c sin α + \sqrt[]{c^{2} sin α + 2 g h}) ... & (2) \end{matrix}

h = 0

, akkor

x = \frac{c^{2} sin 2 α}{g}

b) Hogy ezen kérdésre felelhessünk, indirekt utat választunk^{$^{*}$} nevezetesen keressük, minő hajítási távolságokhoz tartoznak egyáltalában

α

értékek. Ezen célból az eredeti

\begin{matrix} x tg α - \frac{1}{2} \frac{g}{cos^{2} α} x^{2} + h = 0, ill. x tg α = \frac{1}{2} \frac{g}{cos^{2} α} x^{2} - h \end{matrix}

egyenletben

tg α = \frac{sin α}{cos α}

és

x = d

helyettesítése után mindkét oldalon négyzetre emelünk,

sin^{2} α

helyébe (

1 - cos^{2} α

)-t írunk és

cos α

-ra rendezünk. Így keletkezik:

\begin{matrix} 4 c^{4} (h^{2} + d^{2}) cos^{4} α - 4 c^{2} d^{2} (g h + c^{2}) cos^{2} α + g^{2} d^{4} = 0 ... \end{matrix}

(3)

Ezen egyenlet

cos^{2} α

-ra nézve másodfokú és ha valósak a gyökei, pozitívek is, mert szorzatuk és összegük pozitív.^{$^{*}$} A 3) gyökei valósak, ha a discriminánsa nem negatív, tehát ha

\begin{matrix} Δ \equiv 16 c^{4} d^{4} [(g h + c^{2}) - g^{2} (h + d^{2})] = 16 c^{4} d^{4} (c^{4} + 2 g h c^{2} - g^{2} d^{2}) \geq 0. \end{matrix}

Ennek feltétele:

\begin{matrix} g^{2} d^{2} \leq c^{2} (c^{2} + 2 g h) azaz d \leq \frac{c}{g} \sqrt[]{c^{2} + 2 g h} ... \end{matrix}

(4)

Eszerint a legnagyobb hajítási távolság:

\begin{matrix} D = \frac{c}{g} \sqrt[]{c^{2} + 2 g h} ... \end{matrix}

(5)

Ehhez tartozó

α_{m}

hajítási szögre nézve, ha

d

helyett

D

értékét tesszük:

\begin{matrix} cos^{2} α_{m} = \frac{c^{2} D^{2} (g h + c^{2})}{2 c^{4} (h^{2} + D^{2})} = \frac{c^{2} + 2 g h}{2 (c^{2} + g h)} < 1 és tg α_{m} = \frac{c}{\sqrt[]{c^{2} + 2 g h}} ... \end{matrix}

(6)

Innen:

\begin{matrix} \sqrt[]{c^{2} + g h} = c cotg α_{m}, tehát D = \frac{c^{2}}{g} cotg α_{m} ... \end{matrix}

(7)

h = 0

tg α_{m} = 1

α_{m} = 45^{\circ}

. Ha

h > 0

α_{m} < 45^{\circ}

c) Ha

0 < d < D

, akkor

d

ilyen értékéhez

cos^{2} α

-nak két pozitív értéke tartozik

α_{1}

és

α_{2}

. Ezekre nézve 3) alapján

\begin{matrix} cos^{2} α_{1} + cos^{2} α_{2} = \frac{d^{2} (g h + c^{2})}{c^{2} (h^{2} + d^{2})} ... \end{matrix}

(8)

h = 0

cos^{2} α_{1} + cos^{2} α_{2} = 1

, azaz

α_{1} + α_{2} = 90^{\circ}

d) A mozgó pont pályájának egyenletéből

\begin{matrix} y' = tg α - \frac{g}{c^{2} cos^{2} α} x . \end{matrix}

x = O A = d

\begin{matrix} y' = tg α - \frac{g d}{c^{2} cos^{2} α} = tg φ ... \end{matrix}

(9)

ahol

φ

azon szög, melyet a pályának

A

pontban húzott érintője alkot az

X

-tengellyel;

φ

vagy tompaszög, vagy negatív hegyes szög, úgy hogy

tg φ < 0

.
A

γ

szög, amellyel a golyó az

A

ponthoz érkezik, azon szöget jelenti, amelyet az

A

ponthoz tartozó sebesség képez az

X

-tengellyel: ez pedig negatív hegyes szög, úgy hogy

tg γ = tg φ

d = D

esetében:

\begin{matrix} tg φ = tg γ = tg α_{m} - \frac{g}{c^{2} cos^{2} α_{m}} \cdot \frac{c^{2}}{y} cotg α_{m} \\ tg γ tg α_{m} = {tg}^{2} α_{m} - \frac{1}{cos^{2} α_{m}} = {tg}^{2} α_{m} - {sec}^{2} α_{m} = - 1 \\ tg (- γ) tg α_{m} = 1, tehát - γ + α_{m} = 90^{\circ}, γ = - (90^{\circ} - α_{m}) . \end{matrix}

^{$^{*}$}2) szerint

x = O A

α

függvénye és ezen alapon, differenciálással számíthatnánk tovább. E számítás hosszadalmassága miatt választjuk az indirekt utat ezzel közelebb jutunk a következő kérdéshez is.

^{$^{*}$}Még azt is ki kell mutatnunk, hogy a 3) egyenletet kielégítő $cos^{2} α$ értéke 1-nél nem nagyobb. Ezt, mint külön feladatot tűzzük ki.