Kezdőlap


Feladat:	614. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Blahó Miklós , Fekete Ernő , Kail Endre , Kemény György , Királyhidi Gy. , Kiss K. , Komlós János , Mezey Géza , Nagy Elemér , Petricskó Miklós , Rappaport Sándor , Róth Pál , Taussig F. , Weisz Alfréd
Füzet:	1937/szeptember, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Feladat, Prizma, Geometriai optika
Hivatkozás(ok):	Feladatok: 1937/április: 614. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy a prizmára eső $S I$ fénysugár az $N I$ beesési merőlegesnek a hasáb alapja felé eső oldalán halad; a beesés $i$ szöge $= α$ . A prizmába $r$ törésszög alatt behatoló fénysugár az $A B$ lapon $I'$ -nél visszaverődik; ha ezen lapon a beesés szöge $r'$ , a visszaverődés szöge is $r'$ , úgy, hogy $I I' R = 2 r'$ , ahol $R$ az $A C$ lap azon pontja, amelyben a fénysugár elhagyja a prizmát az $N' R S' = i'$ szög alatt. Az $R$ pontban a beesés szöge $I' R N'' = r''$ , a $φ$ határszögnél kisebb tartozik lenni. A prizma anyagára nézve

\begin{matrix} sin φ = \frac{1}{n} = \frac{1}{2} azaz φ \sim 42^{\circ} . \end{matrix}

Tehát

r'' < φ

tartozik lenni. Számítsuk ki

r''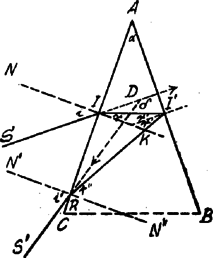

-t.

Minthogy

N K ∥ N' N''

r'' = N K R

. Ez utóbbi az

I I' K Δ

külső szöge, így

\begin{matrix} r'' = \hat{N K R} = r + 2 r' = r + 2 (i - r) = \\ = 2 i - r = 2 α - r . \end{matrix}

Azonban

2 α = 6^{\circ}

és így

2 α - r < φ

.
Áttérhetünk már most a

δ

deviációszög kiszámítására.

δ

I D R Δ

külső szöge, és így

\begin{matrix} δ = \hat{D I R} + \hat{I R D} = 90^{\circ} + i + 90^{\circ} - i' = \\ = 180^{\circ} + α - i' . \end{matrix}

Ha már most figyelemmel vagyunk a törésmutató értékére és arra, hogy a

6^{\circ}

-nál nem nagyobb szögek sinusai helyett az abszolut mérőszámokat vehetjük,

\begin{matrix} \frac{sin i}{sin r} = \frac{i}{r} = n, tehát r = \frac{i}{n} = \frac{α}{n} \end{matrix}

és

\begin{matrix} r'' = 2 α - \frac{α}{n} = 6^{\circ} - 3 \cdot \frac{2}{3} = 4^{\circ} . \end{matrix}

Hasonlóan:

\begin{matrix} i'' = n r'' = 4 \cdot \frac{3}{2} = 6^{\circ} . \end{matrix}

Eszerint

\begin{matrix} δ = 180^{\circ} + 3^{\circ} - 6 = 177. \end{matrix}

Mezey Géza (Ciszterci Szent-Imre g. VII. o. Bp. XI.)

Jegyzet. A deviáció szögének meg nem felelő értelmezése miatt egyes dolgozatokban az eredmény

3^{\circ}

(a helyes

δ

kiegészítője), másokban

357^{\circ}