Kezdőlap


Feladat:	B.3806	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Reiter Viktor
Füzet:	2006/szeptember, 341 - 342. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszögek hasonlósága, Körérintők, Trapézok, Feladat
Hivatkozás(ok):	Feladatok: 2005/március: B.3806

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelölje a körök középpontját $O_{1}$ , illetve $O_{2}$ , sugarukat $r_{1}$ , illetve $r_{2}$ . Mindkét körnek két-két olyan átmérője van, amelynek egyenese érintője a másik körnek. Mivel az átmérő áthalad a kör középpontján, a fent említett egyenesek az $O_{1}$ pontból a $k_{2}$ körhöz, illetve az $O_{2}$ pontból a $k_{1}$ körhöz húzott érintők: $e_{2}$ és $e_{4}$ , illetve $e_{1}$ és $e_{3}$ (1. ábra). Az érintők közül kettőt kiválasztani négyféleképpen lehet, de a centrálisra vonatkozó szimmetria miatt ez lényegében csak két különböző esetet jelent.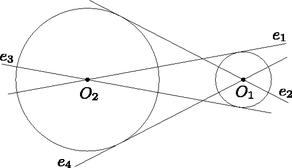

1. ábra

I.) A két kiválasztott egyenes

e_{1}

és

e_{2}

, a vizsgált négyszög

A B C D

(2. 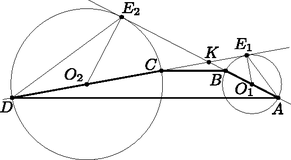ábra).

2. ábra

Itt

E_{1} K O_{1} ∢ = E_{2} K O_{2} ∢

, mert csúcsszögek, és

O_{1} E_{1} K ∢ = O_{2} E_{2} K ∢ = 90^{\circ}

, mert az érintési pontba húzott sugár merőleges az érintőre. Ezért az

O_{1} E_{1} K

és az

O_{2} E_{2} K

háromszög hasonló, mert két-két szögük egyenlő. A hasonlóság aránya:

λ = \frac{r_{1}}{r_{2}}

. Ugyanakkor az

E_{1} A K

és az

E_{2} D K

háromszög is hasonló (szögeik az előző hasonlóság miatt egyenlők). A hasonlóság aránya:

\frac{E_{1} A}{E_{2} D} = \frac{r_{1}}{r_{2}} = λ

.
Így

\frac{A K}{D K} = λ = \frac{2 r_{1}}{2 r_{2}} = \frac{B A}{C D}

, ezért a párhuzamos szelők tételének megfordítása szerint

B C ∥ A D

, tehát a

B A D C

négyszög valóban trapéz.
II.) A két kiválasztott egyenes

e_{2}

és

e_{3}

, metszéspontjuk

M

(3. ábr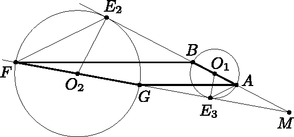a).

3. ábra

Mivel az

M

csúcsnál lévő szög közös, ezért az előző esethez hasonlóan: az

O_{2} E_{2} M

háromszög hasonló az

O_{1} E_{3} M

háromszöghöz, ahol a hasonlóság aránya

λ = \frac{r_{1}}{r_{2}}

; és az

O_{2} E_{2} G

háromszög is hasonló az

O_{1} E_{3} A

háromszöghöz, ahol a hasonlóság aránya szintén

λ = \frac{r_{1}}{r_{2}}

valamint a

G E_{2} M

és az

A E_{3} M

is hasonlóak ugyanilyen arány szerint. Ebből

\frac{M A}{M G} = \frac{A B}{G F}

, így a párhuzamos szelők tételének megfordítása szerint:

A G ∥ B F

, tehát az

A B F G

négyszög ebben az esetben is trapéz.