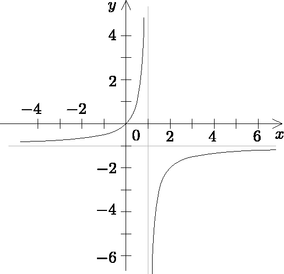Kezdőlap


Feladat:	B.3794	Korcsoport: -	Nehézségi fok: átlagos
Megoldó(k):	Filus Adrienn
Füzet:	2006/március, 149 - 150. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2005/február: B.3794

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azt állítjuk, hogy a bizonyítandó állítás ekvivalens a

\begin{matrix} \frac{p}{1 - p} + \frac{1 - q}{q} > 2 \end{matrix}

(2)

egyenlőtlenséggel. Valóban, (2)-t a feltétel szerint pozitív

(1 - p) q

-val szorozva

\begin{matrix} p q + (1 - p) (1 - q) > 2 q (1 - p) \end{matrix}

adódik, innen pedig a zárójelek felbontása és alkalmas átrendezés után (1)-et kapjuk.
Vegyük észre, hogy az

f (x) = \frac{x}{1 - x}

függvény szigorúan monoton növő a

[0; 1)

intervallumon (ábra). Ez azt jelenti, hogy

f (q) < f (p)

, így pedig (2) bal oldala alulról becsülhető:

\begin{matrix} \frac{p}{1 - p} + \frac{1 - q}{q} > \frac{q}{1 - q} + \frac{1 - q}{q} . \end{matrix}

A kapott egyenlőtlenség jobb oldalán egy pozitív szám és reciprokának összege áll; ismeretes, hogy egy ilyen összeg legalább 2, amiből a bizonyítandó állítás következik.

II. megoldás. Azt igazoljuk, hogy a megadott feltételek esetén az (1) alábbi átrendezésével kapott

\begin{matrix} 3 q - 4 p q = q (3 - 4 p) < 1 - p \end{matrix}

(3)

egyenlőtlenség teljesül. Ha

3 - 4 p \leq 0

, akkor a bal oldal nem pozitív, a jobb oldal pedig a feltétel szerint igen.
Ha

3 - 4 p > 0

, akkor (3) mindkét oldalát ezzel elosztva elegendő igazolni, hogy ha

0 < q < p < \frac{3}{4}

, akkor

\begin{matrix} q < \frac{1 - p}{3 - 4 p} . \end{matrix}

(4)

A befejezés az első megoldás alapötletét hasznosítja: gyorsan adódik, hogy ha

p < \frac{3}{4}

, akkor

\begin{matrix} p \leq \frac{1 - p}{3 - 4 p}, \end{matrix}

(5)

ahonnan a

q < p

feltétel szerint megkapjuk (4)-et.
Az (5) egyenlőtlenséget egyszerűen igazolhatjuk: a jobb oldalon a nevező pozitív, beszorozva rendezés után teljes négyzetet kapunk:

\begin{matrix} 4 p^{2} - 4 p + 1 = {(2 p - 1)}^{2} \geq 0. \end{matrix}

Megjegyzések. 1. Ha a II. megoldás szerint nem a

q

, hanem a

p

változót ,,fejezzük ki'', akkor a

\begin{matrix} 3 q - 1 < p (4 q - 1) \end{matrix}

egyenlőtlenséget kapjuk. Ennek az igazolása azonban nehézkesebb abban az esetben, ha

4 q - 1 < 0

.
2. A feladat nehezebbnek bizonyult a vártnál, elgondolkoztató a hibás dolgozatok magas száma. Ezekben többnyire egyenlőtlenségek során nem megengedett lépések ,,alkalmazása'' volt a hiba.