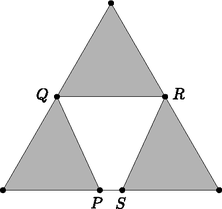Feladat: B.3754 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Csata Árpád ,  Gehér György ,  Kis-Tóth Christian ,  Kisfaludi-Bak Sándor ,  Lovász László Miklós ,  Nagy János ,  Nagy Péter ,  Rácz Miklós 
Füzet: 2005/szeptember, 345 - 346. oldal  PDF  |  MathML 
Témakör(ök): Szabályos sokszögek geometriája, Háromszögek egybevágósága, Lefedések, Feladat
Hivatkozás(ok):Feladatok: 2004/október: B.3754

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Válasszuk az adott H szabályos háromszög oldalát egységnyinek és tegyük föl, hogy az mégis felbontható az egybevágó H1, H2, H3, H4, H5 háromszögekre. Jelöljük a Hi háromszögek csúcsainak a halmazát V-vel.
Azt állítjuk, hogy a H mindhárom oldalának belsejében van V-beli pont. Ha nem így lenne, akkor valamelyik részháromszögnek lenne a H-val közös, egységnyi hosszú oldala. A részek egybevágósága miatt tehát valamennyi részháromszögben lenne egységnyi hosszú oldal. Ismeretes, hogy egy egységnyi oldalú szabályos háromszöglemez pontosan három egységnyi hosszúságú szakaszt tartalmaz; a háromszög oldalait. Ha mármost mind az öt részháromszögnek van egységnyi hosszú oldala, akkor szükségképpen van közös oldala a felbontás két részháromszögének és ez a H belsejében halad, egy ilyen szakasz hossza viszont kisebb a háromszög oldalánál, nem lehet tehát egységnyi.
A felbontásban részt vevő háromszögek szögeinek az összege 5⋅180∘=900∘. Ez az érték a V pontjai körül is kiadódik: ha a V csúcshalmaznak b darab pontja található a H belsejében és k a kerületén, akkor a H csúcsai egyenként 60∘-kal, az oldalak belsejében lévő (k-3) pont mindegyike 180∘-kal, egy-egy belső pont pedig 360∘-kal járul hozzá a szögösszeghez. Így

900∘=3⋅60∘+(k-3)⋅180∘+b⋅360∘,
ahonnan rendezés után kapjuk, hogy 7=k+2b. Láttuk, hogy mindhárom oldal a belsejében is tartalmaz V-beli pontot, így a H csúcsaival együtt k≥6, tehát 2b≤1. Mivel b nemnegatív egész, azért csak b=0 lehetséges. A V halmaznak tehát pontosan hét pontja van, mindegyikük a H kerületén, három a csúcsokban, négy pedig az oldalakon található, mindegyiken legalább egy. A V pontjai tehát az ábra szerinti elrendezésben helyezkednek el H oldalain. Az öt egybevágó rész közül hármat a PQ, QR, RS szakaszok vágnak le a H-ból, a további két részre pedig az egyik átlója vágja szét a PQRS négyszöget.
 
 

Mivel a három satírozott rész egybevágó, bennük az egyenlő, 60∘-os szögekkel szemközt egyenlő oldalak vannak, így PQ=QR=RS. Bármelyik átlót rajzoljuk is meg a PQRS négyszögben, az így adódó két háromszög egyikének vannak egyenlő oldalai. A részháromszögek tehát egyenlő szárúak és mivel van 60∘-os szögük is, szükségképpen szabályosak. Ekkor a PQRS négyszögnek két szomszédos 120∘-os szöge van (a P-nél és az S-nél), egy ilyen négyszöget pedig nem lehet az átlójával két szabályos háromszögre vágni.
A kívánt felosztás tehát valóban nem lehetséges.