Kezdőlap


Feladat:	3788. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gyenis András , Kónya Gábor
Füzet:	2005/december, 558 - 561. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev testek mechanikája, Rugalmatlan ütközések, Feladat
Hivatkozás(ok):	Feladatok: 2005/március: 3788. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A feladat szövege nem utal arra, hogy milyen ütközésről van szó, ezért vizsgáljuk a $k$ ütközési számmal jellemezhető rugalmatlan ütközést (ez $k = 1$ esetén a rugalmas, $k = 0$ -ra pedig a tökéletesen rugalmatlan ütközést is leírja).
Nevezzük a továbbiakban az ütközés előtt is mozgó korongot elsőnek, az állót pedig másodiknak. A korongok tömegét jelöljük $m$ -mel, sugarukat $R$ -rel, és az ütközés pillanatában a korongok középpontját összekötő (centrális) egyenes zárjon be $α$ szöget a $v$ vektor irányával. A csúszási és a tapadási súrlódási együtthatót egyforma, $μ$ nagyságúnak tekintjük.

Megjegyzés. Az

α

szög kifejezhető annak az egyenesnek, amely mentén a sebességgel érkező korong középpontja mozog, valamint az álló korong középpontjának

b

távolságával, az ún. ütközési paraméterrel:

b = 2 R sin α

. Az ütközési paraméter az atomfizikai és részecskefizikai ütközések leírásánál gyakran használt mennyiség, arról ad felvilágosítást, hogy mennyire nem centrális az ütközés.

Az egyszerűség kedvéért tegyük fel, hogy a korongok az ütközés előtt nem forogtak (bár a forgás figyelembe vétele sem jelentene elvi nehézséget). Nem tételezhetjük fel azonban a forgásmentességet az ütközés után, hiszen az egymással súrlódó korongok (a centrális ütközés speciális esetét leszámítva) a két korong között fellépő súrlódási erők forgatónyomatéka miatt szükségszerűen forgásba jönnek.
Írjuk le az ütközést a két korong tömegközépponti koordináta-rendszeréből, vagyis abból a rendszerből szemlélve, amely a talajhoz képest

v / 2

sebességgel mozog. Ebben a rendszerben az első korong ütközés előtti sebessége

v / 2

, a másodiké pedig

- v / 2

. Válasszuk úgy a koordináta-rendszer tengelyeit, hogy az ütközés pillanatában a korongok középpontja az

y

tengelyre, az érintkezési pontjuk pedig az origóba kerüljön (lásd az ábrát).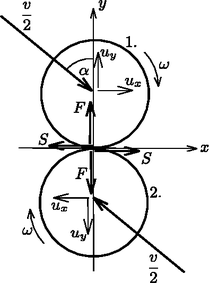

Az első korong ütközés előtti sebességvektorának komponensei:

\begin{matrix} v_{x} = \frac{1}{2} v sin α és v_{y} = - \frac{1}{2} v cos α, \end{matrix}

a másik korongé ennek

(- 1)

-szerese. Jelöljük az első korong ütközés utáni sebességkomponenseit

u_{x}

-szel és

u_{y}

-nal (a másiké ennek

(- 1)

-szeresei lesznek), a korongok szögsebessége pedig legyen az ütközés után

ω

, az ábrán látható irányítással.
Az ütközés (rövid) ideje alatt a két korong találkozási pontjában

y

(sugár) irányban mindkét korongra ugyanakkora nagyságú, de ellentétes irányú

F (t)

erő hat, érintőlegesen (

x

irányban) pedig

S (t)

súrlódási erő. Az ütközés idejét jelöljük

τ

-val, az erőhatások ezen időtartamra vett átlagértékét pedig

F

-fel és

S

-sel.
Az

F

erő hatására a korongok sugár irányú sebessége az eredeti érték

- k

-szorosára változik, ahol

k

az ütközési szám:

\begin{matrix} u_{y} = k \frac{v}{2} cos α, \end{matrix}

(1)

és a dinamika alaptörvénye szerint

\begin{matrix} - m \frac{v}{2} cos α + F τ = k m \frac{v}{2} cos α . \end{matrix}

(2)

Az érintő irányú impulzusváltozásra

\begin{matrix} m \frac{v}{2} sin α - S τ = m u_{x}, \end{matrix}

(3)

a forgási állapot megváltozására pedig a forgómozgás alapegyenletéből

\begin{matrix} \frac{1}{2} m R^{2} \cdot ω = S R τ \end{matrix}

(4)

írható fel. (Kihasználtuk, hogy egy homogén tömegeloszlású korong tehetetlenségi nyomatéka

m R^{2} / 2

Megjegyzés. A (3) és (4) egyenletekből (

S τ

kiküszöbölésével) következik, hogy

\begin{matrix} m \frac{v}{2} R sin α = \frac{1}{2} m R^{2} \cdot ω + m u_{x} R, \end{matrix}

amit közvetlenül (az erőlökések felírása nélkül) is megkaphattunk volna, ha az ütközési pontra vonatkozó perdület megmaradásának törvényét alkalmazzuk.

A további vizsgálódás során két esetet kell megkülönböztetnünk.
I. eset: A súrlódás elegendően nagy ahhoz, hogy a korongok relatív sebessége az érintkezési pontban még az ütközés befejeződése előtt nullára csökkenjen. Ekkor a súrlódási erő is nullára csökken, és az ütközés befejeződéséig nulla is marad, tehát a korongok érintkezési pontjának relatív sebessége is nulla kell legyen az ütközés végén. (Ha nem így lenne, hanem a korongok ismét elkezdenének csúszni egymáson, akkor ,,rossz'', a sebességekkel megegyező irányú súrlódási erővel lehetne csak a mozgást magyarázni, ez pedig lehetetlen!) A korongok ,,összecsiszolódásának'' (az egymáson való tiszta gördülésének) feltétele a sebesség és a szögsebesség között teremt kapcsolatot:

\begin{matrix} u_{x} = R ω . \end{matrix}

(5a)

Mi a feltétele annak, hogy ez az eset következzék be? Az, hogy az átlagos súrlódási erő kisebb legyen, mint az átlagos nyomóerő

μ

-szöröse:

\begin{matrix} S < μ F . \end{matrix}

(6a)

Az (1)‐(4) és

(5 a)

egyenletrendszert megoldva

\begin{matrix} u_{x} & = \frac{1}{3} v sin α, & (7a) \\ u_{y} & = \frac{k}{2} v cos α, & (8a) \\ R ω & = \frac{1}{3} v sin α, & (9a) \\ F τ & = \frac{k + 1}{2} m v cos α, & (10a) \\ S τ & = \frac{1}{6} m v sin α, & (11a) \end{matrix}

(6 a)

feltételből pedig a súrlódási együtthatóra

\begin{matrix} μ > \frac{tg α}{3 (k + 1)} = μ_{krit.} \end{matrix}

(12a)

adódik.

II. eset: A súrlódás nem elegendő ahhoz, hogy a korongok relatív sebessége az érintkezési pontban nullára csökkenjen; ilyenkor a két korong az ütközés egész ideje alatt ,,köszörül'', csúszik egymáson. Ebben az esetben a súrlódási erő és a felületeket összeszorító erő között mindvégig fennáll az

S (t) = μ F (t)

összefüggés, és az átlagértékek között is teljesül

\begin{matrix} S = μ F . \end{matrix}

(5b)

A köszörülés feltétele az, hogy még az ütközési folyamat végén is legyen sebességkülönbség a két érintkező felület között, vagyis fennálljon

\begin{matrix} u_{x} > R ω . \end{matrix}

(6b)

Most az (1)‐(4) és

(5 b)

egyenletrendszert kell megoldanunk:

\begin{matrix} u_{x} & = v [\frac{1}{2} sin α - μ \frac{k + 1}{2} cos α], & (7b) \\ u_{y} & = \frac{k}{2} v cos α, & (8b) \\ R ω & = v \cdot μ (k + 1) cos α, & (9b) \\ F τ & = \frac{k + 1}{2} m v cos α, & (10b) \\ S τ & = \frac{1}{2} m v \cdot μ (k + 1) cos α . & (11b) \end{matrix}

Ellenőrizhetjük, hogy a

(6 b)

feltétel

\begin{matrix} μ < \frac{tg α}{3 (k + 1)} = μ_{krit.} \end{matrix}

(12b)

esetén teljesül.

A tömegközépponti koordináta-rendszerből könnyen visszatérhetünk az eredeti (a talajhoz képest álló) ,,labor-rendszerbe''. Ha

U^{(1)}

-gyel jelöljük az első test sebességvektorát,

U^{(2)}

-vel pedig a másodikét a labor-rendszerben, ezek komponenseire fennáll:

\begin{matrix} U_{x}^{(1)} & = {\begin{matrix} v \frac{5}{6} sin α, & ha μ \geq μ_{krit.}, \\ v (1 - \frac{μ}{6 μ_{krit.}}) sin α, & ha μ \leq μ_{krit.}, \end{matrix} \\ U_{y}^{(1)} & = - v \frac{1 - k}{2} cos α, \\ U_{x}^{(2)} & = {\begin{matrix} v \frac{1}{6} sin α, & ha μ \geq μ_{krit.}, \\ v \frac{μ}{6 μ_{krit.}} sin α, & ha μ \leq μ_{krit.}, \end{matrix} \\ U_{y}^{(2)} & = - v \frac{1 + k}{2} cos α . \end{matrix}

Belátható, hogy a korongok ütközés utáni sebességvektora mindig hegyesszöget, vagy legfeljebb derékszöget zár be egymással. Tanulmányozhatjuk a különböző speciális eseteket is. Például a

k = 1

és

μ ≫ 1

határeset (ekkor sugár irányban tökéletesen rugalmas, érintő irányban viszont tökéletesen rugalmatlan az ütközés) lényegében megegyezik az 1994. évi Nemzetközi Fizikai Diákolimpia 3. elméleti feladatával (lásd KöMaL, 1994. évi 11. szám, 464. oldal).