Kezdőlap


Feladat:	2005. évi Nemzetközi Fizika Diákolimpia 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Tasnási Tamás , Vankó Péter
Füzet:	2005/november, 491 - 494. oldal		PDF \| MathML
Témakör(ök):	Egyéb időben változó mágneses mező, Körvezető mágneses tere, Egyéb elektromos mérőműszerek, Nemzetközi Fizika Diákolimpia
Hivatkozás(ok):	Feladatok: 2005/október: 2005. évi Nemzetközi Fizika Diákolimpia 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás.

Az ohm meghatározása (Kelvin)
1. Az

ω

szögsebességgel egyenletesen forgó

a

sugarú tekercsre feszített felületen a mágneses fluxus az eltelt idő függvényében

Φ (t) = N a^{2} π B_{0} cos ω t

, tehát a tekercsben indukált elektromotoros erő: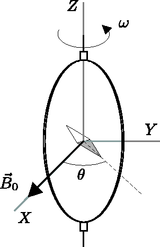

\begin{matrix} E = - \frac{d Φ}{d t} = N a^{2} π B_{0} ω sin ω t . \end{matrix}

A tekercs forgatásához szükséges átlagos teljesítmény megegyezik az

R

ellenállású tekercsben disszipálódott

P (t) = \frac{E^{2} (t)}{R}

pillanatnyi teljesítmény átlagértékével, ami

\begin{matrix} 〈 P 〉 = \frac{1}{T} \int_{t = 0}^{T} P (t) d t = \frac{{(N a^{2} π B_{0} ω)}^{2}}{2 R} . \end{matrix}

A képletben

T = \frac{2 π}{ω}

a forgatás periódusidejét jelöli, és felhasználtuk, hogy

\frac{1}{2 π} \int_{0}^{2 π} sin^{2} x d x = \frac{1}{2}

2. A forgó keretben indukált áram mágneses tere hozzáadódik a külső mágneses térhez, ez okozza az iránytű elfordulását. Számoljuk ki először a tekercs középpontjában a mágneses indukció vektor pillanatnyi értékét, majd az egyes komponensek időátlagát. A középpontban elhelyezett iránytű a mágneses tér időátlagát érzékeli.
Jelölje az egyes koordinátatengelyek irányába mutató egységvektorokat rendre

\vec{i}

\vec{j}

és

\vec{k}

. A

t

időpillanatban a forgó keret normálisa éppen

ω t

szöget zár be az

x

tengellyel, így a keret közepén a tekercsben folyó áram által keltett mágneses indukció az idő függvényében

\begin{matrix} B (t) = \frac{μ_{0} N I (t)}{2 a} (cos ω t \cdot \vec{i} + sin ω t \cdot \vec{j}), ahol I (t) = \frac{E (t)}{R} = \frac{N a^{2} π B_{0} ω}{R} sin ω t \end{matrix}

a keretben folyó áram pillanatnyi értéke.
Így, figyelembe véve a

B_{0} = B_{0} \vec{i}

külső mágneses indukciót is, a mágneses indukció egyes komponenseinek átlagértékére a következőket kapjuk:

\begin{matrix} 〈 B_{x} 〉 & = B_{0} + \frac{μ_{0} N^{2} a π B_{0} ω}{2 R} 〈 cos ω t sin ω t 〉 = B_{0}, \\ 〈 B_{y} 〉 & = \frac{μ_{0} N^{2} a π B_{0} ω}{2 R} 〈 sin^{2} ω t 〉 = \frac{μ_{0} N^{2} a π B_{0} ω}{4 R} . \end{matrix}

(Az átlagértékek kiszámításánál felhasználtuk, hogy

sin x cos x = \frac{1}{2} sin 2 x

, aminek az átlaga zérus, és

sin^{2} x = \frac{1}{2} (1 - cos 2 x)

, aminek az átlaga

\frac{1}{2}

.)
A mágnestű az átlagtér irányába áll be, tehát az

x

tengellyel bezárt

θ

szögére

tg θ = \frac{〈 B_{y} 〉}{〈 B_{x} 〉}

adódik, ahonnan a keresett ellenállás:

\begin{matrix} R = \frac{μ_{0} N^{2} a π ω}{4 tg θ} . \end{matrix}

Érdekes, hogy a kapott eredmény nem függ a külső mágneses tér

B_{0}

nagyságától.
A fenti problámával lényegében azonos a Gnädig Péter ‐ Honyek Gyula: 123 Furfangos fizika feladat című könyvében található 108. feladat.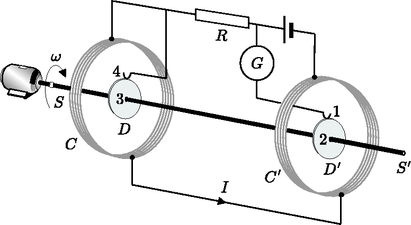

Az ohm meghatározása (Rayleigh, Sidgwick)

3. Az

a

sugarú,

N

menetes

C

és

C'

tekercsek középpontjukban

B = \frac{μ_{0} N I}{2 a}

nagyságú, tengelyirányú mágneses teret hoznak létre. Ebben a térben

ω

szögsebességgel forgó fém korongban levő elektronokra sugár irányban hat a Lorentz-erő, melynek nagysága a tengelytől mért

r

távolság függvényében

F_{L} (r) = q_{e} r ω B

, ahol

q_{e}

az elektron töltése. Mivel a korongok sugara

b ≪ a

, feltehetjük, hogy a mágneses tér közel homogén a tengely közelében. A Lorentz-erő hatására a fém korongban levő szabad elektronok sugár irányban elmozdulnak, és olyan radiális

E (r)

elektrosztatikus teret hoznak létre, mely a Lorentz-erő hatását kiegyenlíti, azaz

E (r) = \frac{F_{L} (r)}{q_{e}}

. Ez az elektromos tér okozza a korong közepe és pereme között fellépő feszültséget, melynek értéke:

\begin{matrix} E_{D} = \int_{r = 0}^{b} E (r) d r = \int_{r = 0}^{b} r ω B d r = \frac{μ_{0} N I b^{2} ω}{4 a} . \end{matrix}

Mivel a

C

és

C'

tekercsek mágneses tere ellentétes irányú, de ugyanakkor a két korong is ellentétes értelemben van sorba kapcsolva, az

1

-es és

4

-es pont között mérhető elektromotoros erő

E = E_{D} - E_{D'} = 2 E_{D} = \frac{μ_{0} N I b^{2} ω}{2 a}

Megjegyzés. Esetleg sok megoldónak segíthet, ha a forgó korongok helyett küllős kereket képzelnek, és megpróbálják meghatározni a homogén mágneses térben mozgó küllőkben indukált feszültséget. Ez az általános indukciós törvény értelmében megegyezik az időegység alatt súrolt fluxussal:

| E_{D} | = | \frac{d Φ}{d t} | = B \frac{b^{2} ω}{2}

, összhangban az integrálással kapott eredménnyel.

A fenti problémával rokon a 123 Furfangos fizika feladat című könyv 110. feladata.
4. Ha a

G

galvanométer nullát mutat, akkor ebben az ágban nem folyik áram, tehát a tekercsek

I

árama halad át a vizsgált

R

ellenálláson is. Az ellenálláson eső

R I

feszültség megegyezik az előbb kiszámolt

E

elektromotoros erővel, ahonnan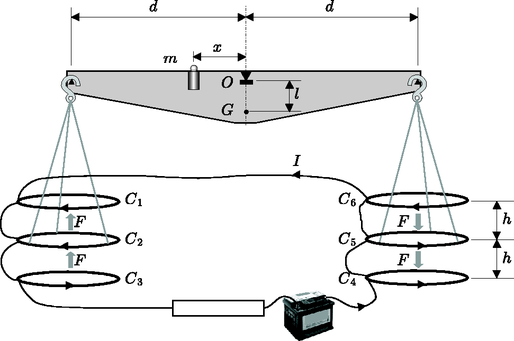

R = \frac{μ_{0} N b^{2} ω}{2 a}

Az amper meghatározása

5. A végtelen hosszú,

I_{1}

árammal átjárt egyenes vezető

r

távolságban

B_{1} (r) = \frac{μ_{0} I_{1}}{2 π r}

mágneses teret hoz létre, ami hosszegységenként

\begin{matrix} f (r) = B_{1} (r) I_{2} = \frac{μ_{0} I_{1} I_{2}}{2 π r} \end{matrix}

erővel hat az első vezetővel párhuzamos,

I_{2}

árammal átjárt vezetőre. Esetünkben

I_{1} = I_{2} = I

, a két vezető távolsága

r = h

, és a körvezető hossza

2 π a

, tehát a két szomszédos tekercs között ható

F (h)

erő:

\begin{matrix} F (h) = 2 π a f (h) = \frac{μ_{0} a I^{2}}{h} . \end{matrix}

6. A mérleg két serpenyőjére ható erők együtt

4 F d

forgatónyomatékot fejtenek ki a mérleg karjára, hiszen mindkét serpenyőre

2 F

erő hat, és mindkét erő azonos

d

erőkaron azonos irányba forgatja a mérleg karját. Egyensúlyban ezt a forgatónyomatékot a mérleg karján elhelyezett

m

tömeg

m g x

forgatónyomatéka kiegyenlíti, tehát

\begin{matrix} m g x = 4 F d = \frac{4 μ_{0} a d I^{2}}{h}, ahonnan I = \frac{1}{2} \sqrt[]{\frac{m g x h}{μ_{0} a d}} . \end{matrix}

7. Térítsük ki a mérleg karját a vízszinteshez képest kicsiny

δ φ

szöggel, és vizsgáljuk meg, hogy a karra mekkora

δ φ

kitérés esetén hat visszatérítő forgatónyomaték!

A mérlegre ható nehézségi erő a kitérést ellensúlyozni igyekszik, és forgatónyomatéka

M g l sin δ φ

. A serpenyőkre ható külső tekercsek forgatónyomatéka

\begin{matrix} 2 d (F (h + δ z) + F (h - δ z)), ahol δ z = d sin δ φ \end{matrix}

a mérlegserpenyők függőleges elmozdulása, hiszen mindkét oldalon a serpenyők az egyik rögzített tekercshez

δ z

-vel közelebb, a másik rögzített tekercstől pedig

δ z

-vel távolabb kerülnek. Az

m

tömegű test forgatónyomatéka kis

δ φ

szög esetén gyakorlatilag (

δ φ

-ben első rendben) nem változik, értéke marad

m g x

. (A mérlegkar elfordulásával mind az

x

, mind a

d

erőkar

cos δ φ

-szeresére csökken, ez az effektus azonban kis

δ φ

-re elhanyagolható, hiszen

cos δ φ \approx 1 - \frac{1}{2} {(δ φ)}^{2}

, ami másodrendűen kicsiny hatás.) Így a kitérített mérlegkar akkor fordul vissza eredeti egyensúlyi helyzete felé, ha

\begin{matrix} M g l sin δ φ > 2 d (F (h + δ z) + F (h - δ z)) - m g x . \end{matrix}

Használjuk fel az 5. és 6. alkérdésre kapott eredményeket, továbbá alkalmazzuk a

\begin{matrix} sin δ φ \approx δ φ \approx \frac{δ z}{d}, és \frac{1}{h \pm δ z} \approx \frac{1}{h} (1 \mp \frac{δ z}{h} + {(\frac{δ z}{h})}^{2}) \end{matrix}

közelítéseket. Ekkor azt kapjuk, hogy

\begin{matrix} \frac{M g l δ z}{d} > \frac{4 μ_{0} a d I^{2} {(δ z)}^{2}}{h^{3}}, ahonnan δ z < \frac{M g l h^{3}}{4 μ_{0} a d^{2} I^{2}} = \frac{M l h^{2}}{m x d} . \end{matrix}