Kezdőlap


Feladat:	3751. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hagymási Imre
Füzet:	2005/április, 240 - 242. oldal		PDF \| MathML
Témakör(ök):	Körvezető mágneses tere, Feladat
Hivatkozás(ok):	Feladatok: 2004/november: 3751. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A Biot‐Savart-törvény szerint egy $I$ erősségű egyenárammal átjárt (zárt) vezető mágneses tere a vezető kicsiny darabkákra történő felosztásával és az egyes darabkák járulékainak összegzésével kapható meg. Egy $Δ l$ hosszúságú (egyenesnek tekinthető) vezető-darabka a tőle $r$ távolságban levő $P$ pontban

\begin{matrix} Δ B = \frac{μ_{0}}{4 π} \frac{I Δ l}{r^{2}} sin α \end{matrix}

nagyságú mágneses indukció járulékot hoz létre, ahol

α

a vezetődarabka és a tőle a

P

pontba mutató

r

vektor által bezárt szög.

Δ B

iránya merőleges mind a vonaldarabra, mind pedig az

r

vektorra. Vektoros jelölésekkel

\begin{matrix} B = \sum Δ B = \frac{μ_{0} I}{4 π} \sum \frac{Δ l \times r}{r^{3}} . \end{matrix}

Ennek alapján az

R

sugarú köráram középpontjában a mágneses indukció nagysága:

\begin{matrix} B_{0} = \frac{μ_{0} I}{4 π} \sum \frac{Δ l}{R^{2}} sin 90^{\circ} = \frac{μ_{0} I}{4 π R^{2}} \sum Δ l = \frac{μ_{0} I}{4 π R^{2}} 2 R π = \frac{μ_{0} I}{2 R} . \end{matrix}

Hasonló módon ‐ viszonylag könnyen ‐ kiszámíthatjuk a körvezető síkjára merőleges szimmetriatengely bármely pontjában a mágneses indukció értékét. A kör középpontjától

r

távolságban a tengely mentén (

r ≫ R

esetben) az indukcióvektor nagysága:

\begin{matrix} B_{1} = \frac{μ_{0} I R^{2}}{2 {(r^{2} + R^{2})}^{3 / 2}} \approx \frac{μ_{0} I R^{2}}{2 r^{3}} . \end{matrix}

Ez ugyan még nem a feladatban szereplő ‐ a köráram síkjában mérhető ‐ indukció, de attól csak egy 2-es szorzótényezőben különbözik, kétszer nagyobb annál. Ezt pl. úgy láthatjuk be, hogy köráramtól távoli mágneses dipóltér helyett egy elektromos dipólus (két egymáshoz közeli, azonos nagyságú, de ellentétes előjelű töltés) elektromos erőterét vizsgáljuk.
Az 1. ábrán látható dipólus térerőssége a tengelye mentén fekvő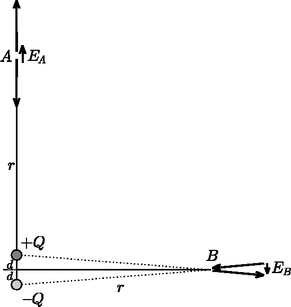

A

pontban

(r ≫ d)

\begin{matrix} E_{A} = k q (\frac{1}{{(r - d)}^{2}} - \frac{1}{{(r + d)}^{2}}) = k Q \frac{4 r d}{r^{2} - d^{2}} \approx 2 k \frac{2 Q d}{r^{3}} . \end{matrix}

Hasonlóan a dipól tengelyére merőlegesen elhelyezkedő

B

pontban:

\begin{matrix} E_{B} \approx k \frac{2 Q d}{r^{3}} = \frac{1}{2} E_{A} . \end{matrix}

1. ábra

Az elektromos és a mágneses dipólterek hasonlósága miatt megállapíthatjuk, hogy a feladatunkban szereplő

B

és a Biot‐Savart-törvényből kiszámított

B_{1}

aránya is

1 / 2

, így tehát a kérdéses arány: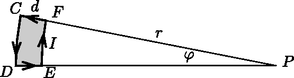

\begin{matrix} \frac{B_{0}}{B} = 2 \frac{B_{0}}{B_{1}} = 2 \cdot \frac{r^{3}}{R^{3}} . \end{matrix}

II. megoldás. Induljunk ki abból a tényből, hogy egy síkbeli zárt vezető által létrehozott mágneses mező a vezetőtől távol egy pontszerű mágneses dipólus terével egyezik meg, és ennek a dipólusnak az erőssége (ún. mágneses dipólnyomatéka) a vezetőben folyó áramnak és a vezető által határolt területnek a szorzata. Ha tehát a köráramot helyettesítjük egy más alakú (kényelmesebben kezelhető) áramvezetővel, amelynek a területe ugyanakkora, mint az eredeti köráramé (vagyis

R^{2} π

), és a benne folyó áram erőssége is megegyezik a feladatban szereplő köráraméval, akkor a mágneses terük ‐ legalábbis a vezetőktől távol ‐ ugyanolyan lesz.

2. ábra

Tekintsük a 2. ábrán látható kicsiny ‐ körgyűrű-cikk alakú ‐ áramvezetőt, és számoljuk ki a mágneses terét a körcikk

P

középpontjában! A Biot‐Savart-törvény szerint az

D E

és

F C

szakaszok nem adnak járulékot a

P

pontbeli mágneses térhez (hiszen

sin α = 0

), a két körív járuléka pedig

\begin{matrix} B = \frac{μ_{0} I}{4 π} (\sum_{(r)}^{} \frac{Δ l}{r^{2}} - \sum_{(r + d)}^{} \frac{Δ l}{{(r + d)}^{2}}) = \frac{μ_{0} I}{4 π} (\frac{r φ}{r^{2}} - \frac{(r + d) φ}{{(r + d)}^{2}}) \approx \frac{μ_{0} I}{4 π} \frac{φ d}{r^{2}} . \end{matrix}

Használjuk most ki, hogy a kicsiny körgyűrű-cikk területe meg kell egyezzék a körvezető területével:

\begin{matrix} d \cdot r φ = R^{2} π, \end{matrix}

ahonnan a kérdéses mágneses indukció nagysága:

\begin{matrix} B = \frac{μ_{0} I R^{2}}{4 r^{3}}, \end{matrix}

összhangban az I. megoldásban kapott eredménnyel.

Megjegyzések. 1. Sokan megpróbálták a Biot‐Savart-törvény segítségével ‐ az integrálszámítás összefüggéseinek felhasználásával ‐ meghatározni a

B

mágneses indukció értékét a köráram síkjában, a középponttól nagy távolságban. Ezt általában közelítő számítással tették, de az eredményük ‐ logikusnak tűnő, ám mégis hibás feltevések miatt ‐ nem egyezett meg a helyes aránnyal. A leggyakoribb hiba az volt, hogy a Biot‐Savart-törvény nevezőjében szereplő (helyről helyre változó) távolságot

r ≫ R

-re hivatkozva állandónak tekintették. Ez csak közelítőleg igaz, és a közelítés éppen egy kettes faktorral változtatja meg a számolás eredményét.
2. Többen nem a köráram síkjában fekvő, hanem a síkra merőlegesen elhelyezkedő

r

távolságú pontban vizsgálták a mágneses indukciót, tehát nem a feladatban feltett kérdésre válaszoltak; munkájuk erősen hiányos.
3. Hagymási Imre (Debrecen, DE Kossuth L. Gyak. Gimn., 12. o.t.) felírta a körvezető mágneses terét megadó formulákat (ún. első- és másodfajú elliptikus integrálokat), majd ezek nagy távolságban érvényes alakjának segítségével numerikusan helyesen meghatározta a kérdéses arányt. Számolása a felsőbb matematika technikai részleteiben járatlan olvasónak nem túl tanulságos, ezért itt nem közöljük. Az ilyen módszerek alkalmazása a pontversenyben megengedett ugyan, de nem kötelező; a kitűzött feladatok elemi(bb) módszerekkel is megoldhatók.