Kezdőlap


Feladat:	B.3796	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baranyai J. Attila , Bogár Péter , Csizmadia János , Estélyi István , Gehér György , Gombkötő Tamás , Horváth Zoltán , Ildrin Gasimov , Kisfaludi-Bak Sándor , Kiss-Tóth Christián , Komáromy Dani , Kónya Gábor , Korándi Dániel , Kornis Bence , Kovács Péter , Kunovszki Péter , Kutas Sándor , Petényi Franciska , Poronyi Balázs , Rácz Miklós , Sommer Dániel , Strenner Balázs , Ureczky Bálint
Füzet:	2006/május, 290 - 292. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Szögfelező egyenes, Háromszög nevezetes körei, Inverzió, Feladat
Hivatkozás(ok):	Feladatok: 2005/február: B.3796

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A$ ponton átmenő szelő $e$ , ami az adott kört a $B$ és a $C$ pontban metszi. A $k$ kör középpontja legyen $O$ , az $e$ tükörképe $O A$ egyenesére $e'$ , $B$ , illetve $C$ tükörképe pedig $B'$ , illetve $C'$ . A tükrözés miatt 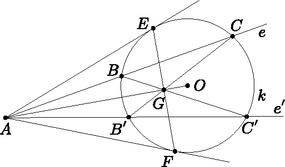$B' G E ∢ = B G F ∢$ és $C' G E ∢ = C G F ∢$ .

1. ábra

Ezért a bizonyítandó állítással ekvivalens, hogy

B G F ∢ = C' G E ∢

, ami éppen azt jelenti, hogy

G

B C'

szakaszon van.
Tehát a szimmetria miatt azt kell megmutatnunk, hogy

B C'

és

B' C

metszéspontja (legyen

P

) egybeesik a

G

ponttal, azaz

P

helyzete független az

e

-nek az

O A

-val bezárt

α

szögétől.
Rögzítsük

e

-t egy tetszőleges helyzetben, amely nem azonos

A O

-val (hiszen akkor a feladat állítása nyilvánvalóan teljesül ‐ 2. ábra). Alkalmazzuk a szögfelező-tételt az

A B C'

háromszögre:

\begin{matrix} \frac{A B}{A C'} & = \frac{P B}{P C'} \Rightarrow & (1) \\ \Rightarrow \frac{P B}{A B} & = \frac{P C'}{A C'} = \frac{P C}{A C} = \frac{P B'}{A B'}; \end{matrix}

az utolsó két egyenlőség az előbbiből és az

A O

-ra vonatkozó tengelyes szimmetriából következik.

2. ábra

Az (1) szerint a páronként különböző

B

C

B'

és

C'

pontok rajta vannak

A P

egyik Apollóniusz-körén, de ugyanakkor az adott

k

körön is, ami csak úgy lehetséges, ha a két kör egybeesik. Legyenek

X

és

Y

A O

egyenesének a körrel való metszéspontjai, ekkor tehát

\frac{P X}{X A} = \frac{P Y}{Y A}

. Írjuk fel az itt szereplő szakaszokat a kör

r

sugarának segítségével:

\begin{matrix} \frac{r - O P}{O A - r} = \frac{r + O P}{O A + r}, ami átrendezve: O P = \frac{r^{2}}{O A} . \end{matrix}

Ebből már látszik, hogy

O P

csak

r

-től és

O A

-tól függ,

α

-tól nem, amit bizonyítani akartunk. Könnyen belátható (pl. az

O E A

derékszögű háromszög

O E

befogójára felírt befogótétel segítségével), hogy ez a pont egybeesik a

G

ponttal.

II. megoldás. Legyen ismét a

k

kör középpontja

O

, sugara

r

E

és

F

egymás tükörképei az

A O

egyenesre nézve, ezért

A O

merőleges

E F

-re; ugyanakkor

A E

merőleges

E O

-ra, mivel

A E

érintő.
A befogótétel alapján

r^{2} = E O^{2} = A O \cdot G O

. Mivel

A

G

és

O

kollineárisak, ez azt jelenti, hogy az

A

és

G

pontok egymás inverzei a

k

alapkörre nézve.

3. ábra

Jelölje továbbra is

e

B C

egyenest. Az inverzió ismert tulajdonságai alapján

e

inverze a

k

körre nézve a

B C O

háromszög köréírt köre (kivéve az

O

pontot), legyen ez az

ℓ

kör. Mivel

A

illeszkedik

e

-re és

A

inverze a

k

körre nézve

G

, azért

G

rajta van az

ℓ

körön. Így a

B C O G

négyszög húrnégyszög.

A G B ∢ = O C B ∢ (= φ

), mivel mindkét szög

180^{\circ}

-ra egészíti ki a

B G O

szöget. (Az egyik mellékszög, a másik pedig a húrnégyszögek tétele szerint.)
A

B C O

háromszög egyenlő szárú, hiszen

B O = C O = r

; így

\begin{matrix} O B C ∢ = O C B ∢ = φ . \end{matrix}

Mivel

B C O G

húrnégyszög, az

O C

oldal a

B

és a

G

csúcsokból ugyanakkora szög alatt látszik:

O G C ∢ = O B C ∢ = φ

. Tehát

A G B ∢ = O C B ∢ = O B C ∢ = O G C ∢ = φ

, ezért

B G F ∢ = 90^{\circ} + φ = C G F ∢

.
Ez azt jelenti, hogy az

E F

egyenes valóban felezi a

B G C

szöget.