| Feladat: | 1962. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1962/október, 49 - 51. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Mozgással kapcsolatos szöveges feladatok, Elsőfokú (és arra visszavezethető) egyenletek, Egyenletek grafikus megoldása, Arany Dániel | ||
| Hivatkozás(ok): | Feladatok: 1962/szeptember: 1962. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 2. feladat. Két autó, ,,'' és elindul egyik városból a másikba. Az első percben egyenlő utat tettek meg. Ekkor motorhiba miatt kénytelen volt sebességét -ére csökkenteni, és így perccel a továbbra is egyenletes sebességgel haladó ,,'' után ért a célba. Ha a hiba -rel távolabb következik be, akkor csak perccel ,,'' után ért volna a célba. Milyen távol van a két város? I. megoldás. Jelöljük az autók induló pontját -vel, célját -vel, a hiba helyét -val és a feltevés szerinti hiba helyét -gal. Legyen továbbá sebessége percenként km, a teljes út megtételéhez szükséges ideje perc. Ekkor -nek az első 5 perc utáni út megtételére, mivel sebességét a 2/5-ére csökkentette, az számára szükséges perc helyett ennek 5/2-ére, percre van szüksége, és ez 15 perccel több, mint amennyi alatt elért -be, tehát Ha motorhibája 4 km-rel távolabb következik be, akkor az addig megtett út . A hiba után hátralevő út . Ezt perc alatt, pedig Most már a két város távolsága . Mindezek szerint motorhibája út után következett be, és akkor még útja volt hátra. új sebessége lett, ezzel a szakaszt perc alatt tette meg. Teljes menetideje perc, késése -hoz képest valóban 15 perc. ‐ Ha viszont a hiba csak út után lépett volna fel, akkor teljes menetideje hasonlóan II. megoldás. Elegendő csak a autóról beszélnünk. Ez az egész úton kezdeti sebességével haladva 15 perccel hamarabb tenné meg az utat, mint úgy, hogy 5 perc után 2/5-ére csökkentette sebességét, ‐ és 10 perccel előbb, mint ha ez a sebességcsökkenés csak 4 km-rel távolabb következik be. Eszerint 4 km út megtételéhez kell 5 perccel hosszabb idő a csökkentett sebességgel, mint az eredeti sebességgel. Így a 15 perc késés 12 km úton következik be, tehát az első 5 percnyi autózás után még ennyit kellett megtenni. Könnyen kiszámíthatjuk másrészt, az első 5 perc után megtett úthoz szükséges időt is. Ezt az utat 5/2-szer akkora idő alatt tette meg csökkentett sebességgel, mint amennyi az indulási sebesség mellett lett volna szükséges, így a késés az eredetileg szükséges idő 3/2-szerese (másfélszer akkora). Az eredeti sebességgel tehát ezt az utat 10 perc alatt tette volna meg. Mivel megállapítottuk, hogy ez az út 12 km, így az első 5 perc alatt 6 km-t hagyott a háta mögött; az egész útja tehát 18 km volt. 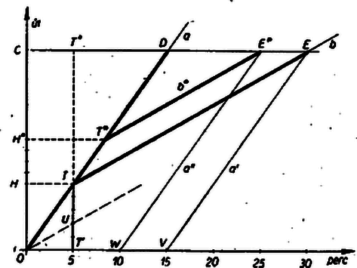 Megjegyzés. A fenti eredmények ismeretében megrajzolhatjuk a mozgások grafikonját. Az ábrán mozgását az egyenesszakasz, mozgását az megtört vonaldarab ábrázolja, a gondolt változatot pedig az megtört vonaldarab. Ehhez az ábrához azonban az előbbi eredményektől függetlenül is eljuthatunk, csak az út-tengely egységének megállapítását kell későbbre halasztanunk, illetőleg éppen ez lesz a feladat. A mozgását mindenesetre egy az -ból kiinduló (tetszés szerinti) ferde egyenes ábrázolja. Ennek az idő-tengely 5 percet ábrázoló pontja fölötti pontja . Megszerkesztve a szakasznak azt az pontját, amelyre , az irányban megkapjuk a további sebességének megfelelő irányt; ha ugyanis mindjárt csökkentett sebességgel indult volna, akkor mozgását az egyenes ábrázolná. Eszerint -t a -n átmenő, -val párhuzamos egyenes adja. Gondoljunk most egy olyan az -val megegyezően mozgó harmadik autót, amely később indul -ből és éppen -ben éri utol -t. Mivel a -ben 15 percet késett -hoz képest, azért ez áll -re is, tehát mozgásának grafikonja az idő-tengely 15 percet ábrázoló pontjából indul ki és párhuzamos -val. Eszerint az pontot és metszése határozza meg, az út-tengely pontját pedig az -n átmenő, az idő-tengellyel párhuzamos egyenes metszi ki. (Ezen van természetesen is.) ‐ Hasonlóan kapjuk annak az gondolt negyedik autó mozgásának grafikonját, amely -val megegyezően mozogva akkor érne -vel együtt -be, ha a motorhiba később következett volna be: ez -n át párhuzamos -val, ahol megfelel a későbbi hibájához tartozó 10 perces késésnek. Így -ot és az egyenes metszéspontja adja, -ból pedig visszafelé, -vel párhuzamosan megrajzolhatjuk annak a mozgásnak a grafikonját, amelyet a feltevés szerint végzett volna a későbbi hibától a célig (-ot a metszi ki -ból). Mivel pedig a és -nak az út-tengelyen levő , ill. vetületei közti távolság 4 km-t ábrázol, a negyedrészét megszerkesztve megkapjuk az út-tengely (1 km-nek megfelelő) mértékegységét. Evvel megmérve az szakaszt, megkapjuk a távolság keresett mértékszámát. Az ábrán a II. megoldás számításainak szemléletes megfelelőit is láthatjuk. , ezért , így , ; másrészt , ezért , . Továbbá -nek -n levő vetületét -vel jelölve , , tehát . |