Kezdőlap


Feladat:	B.3786	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Blázsik Zoltán , Cseh Ágnes , Gehér György , Gyenizse Gergő , Hujter Bálint , Kisfaludi-Bak Sándor , Kiss-Tóth Christian , Klimaj Zoltán , Korándi Dániel , Kornis Bence , Kutas Péter , Lorántfy Bettina , Lovász László Miklós , Mészáros Gábor , Nagy Csaba , Nagy Péter , Németh Zsolt , Rácz Miklós , Strenner Balázs , Szabó Tamás , Szilágyi Csaba , Tomon István , Tossenberger Anna , Udvari Balázs
Füzet:	2005/december, 533 - 534. oldal		PDF \| MathML
Témakör(ök):	Számsorozatok, Számhalmazok, Részhalmazok, Feladat
Hivatkozás(ok):	Feladatok: 2005/január: B.3786

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A kitűzött feladatnál általánosabban azt igazoljuk, hogy ha egy $n$ elemű $H$ számhalmazt kétféleképpen osztunk egy-egy $k$ és $m$ elemű részre, tehát $H = A \cup B = A' \cup B'$ , ahol $| A | = | A' | = k$ és $| B | = | B' | = m$ és $k + m = n$ és az egyes részhalmazok elemeit növekvően rendezzük, tehát $A 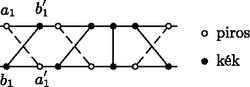= {a_{i} : i = 1,2, ..., k}$ , $A' = {a'_{i} : i = 1,2, ..., k}$ , $B = {b_{j} : j = 1,2, ..., m}$ , $B' = {b'_{j} : j = 1,2, ..., m}$ , akkor

\begin{matrix} | a_{1} - a'_{1} | + | a_{2} - a'_{2} | + ... + | a_{k} - a'_{k} | = | b_{1} - b'_{1} | + | b_{2} - b'_{2} | + ... + | b_{m} - b'_{m} | . \end{matrix}

Vegyünk föl két párhuzamos számegyenest és jelöljük meg mindkettőn a

H

halmaz elemeit. Az első számegyenesen az első felosztás szerint színezzük ki az

A

halmaz elemeit pirosra, a

B

halmaz elemeit pedig kékre, a másodikon pedig az

A'

halmaz elemeit színezzük pirosra és a

B'

halmaz elemeit kékre. Így fent és lent

k

‐

k

darab piros és

m

‐

m

darab kék pontot kapunk. Az azonos sorszámú piros pontokat kössük össze egy-egy piros, az azonos sorszámú kék pontokat pedig egy-egy kék szakasszal. Így egy efféle ábrát kapunk:

Ekkor a részhalmazok rendezése miatt sem a piros, sem pedig a kék szakaszok nem metszik egymást. Ha a piros összeg

P = | a_{1} - a'_{1} | + | a_{2} - a'_{2} | + ... + | a_{k} - a'_{k} |

, a kék összeg pedig

K = | b_{1} - b'_{1} | + | b_{2} - b'_{2} | + ... + | b_{m} - b'_{m} |

, akkor állításunk szerint

P = K

.
Legyen

x \in H

tetszőleges és nézzük meg az

x

színezését fent és lent. Ha

x

fent is és lent is piros, azaz

x \in A \cap A'

, akkor

x

nem szerepel a kék összegben. Ha

x

két példányát ‐ piros ‐ szakasz köti össze, az a piros összegben

| x - x | = 0

tagot jelent. Ha pedig

x

piros ,,szomszédai'' az ábra szerint

z \in A'

, illetve

y \in A

, akkor az abszolút érték felbontása után a piros összegben

(y - x) + (x - z)

adódik, az

x

tehát kiesik. Eszerint ha

x

mindkét példánya piros, akkor az abszolút értékeket felbontva és összevonva az ellenkező előjelű azonos abszolút értékű tagokat

x

sem a piros, sem pedig a kék összegben nem szerepel.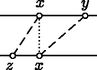

Ugyanez a helyzet, ha

x \in B \cap B'

, azaz

x

mindkét példánya kék.
Nézzük meg, mi történik, ha

x

két példánya különböző színű, mondjuk fent piros, lent pedig kék (

x \in A \cap B'

). Ekkor

x

piros példányából egy piros, kék példányából pedig egy kék szakasz indul. Azt állítjuk, hogy ez a két szakasz metszi egymást, az abszolút érték felbontása után tehát

x

két példánya azonos előjellel szerepel a piros és a kék összegben. Ez pedig már elég a bizonyítandó egyenlőséghez.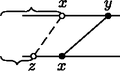

Ha az

x

felső piros példányából induló piros szakasz mégsem metszené az

x

alsó kék példányából induló kék szakaszt, akkor föltehető, hogy ez a két szakasz az ábrán látható módon helyezkedik el, tehát

z < x < y

. Ekkor viszont a felső számegyenes

x

-nél nem nagyobb

H

-beli pontjaiból induló valamennyi szakasz alsó végpontja az

x

-től balra helyezkedik el: a piros szakaszoké azért, mert egyikük sem metszheti a piros

x z

szakaszt, a kékeké pedig azért, mert egyikük sem metszheti a kék

x y

szakaszt. Ez viszont nem lehetséges, mert így a

H

halmaznak ugyanannyi

x

-nél nem nagyobb eleme volna fent, mint ahány

x

-nél kisebb eleme lent. Az

x

piros és kék példányából induló szakaszok tehát valóban metszik egymást, ezzel a bizonyítást befejeztük.