Kezdőlap


Feladat:	B.3783	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bárd Miklós , Majoros Csilla
Füzet:	2005/október, 414 - 415. oldal		PDF \| MathML
Témakör(ök):	Konvex sokszögek, Síkgeometriai számítások trigonometria nélkül, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 2005/január: B.3783

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje $P$ az $A E$ szakasz azon pontját, amelyre $A P = A B$ és így $P E = E D$ teljesül. Legyen $C P = d$ , $A P C ∢ = α$ , $E P C ∢ = β$ .

A B C

és az

A P C

háromszögben két-két oldal hossza egyenlő, ezért

d > 1 \Leftrightarrow α < 90^{\circ}

és

d < 1 \Leftrightarrow α > 90^{\circ}

. Hasonlóan, a

C P E

és a

C D E

háromszögek összevetéséből

d > 1 \Leftrightarrow β < 90^{\circ}

és

d < 1 \Leftrightarrow β > 90^{\circ}

. Így

d > 1

esetén

180^{\circ} = α + β < 90^{\circ} + 90^{\circ} = 180^{\circ}

d < 1

esetén pedig

180^{\circ} = α + β > 90^{\circ} + 90^{\circ} = 180^{\circ}

; mindkettő lehetetlen, ezért

d = 1

, tehát az

A B C

és az

A P C

, valamint a

C P E

és a

C D E

háromszögek egybevágók. Az ötszög területe így az

A B C

és a

C D E

háromszög terület-összegének a kétszerese; ha

A 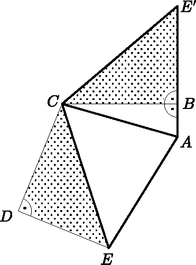P = A B = x

, akkor

\begin{matrix} 2 (\frac{x \cdot 1}{2} + \frac{(1 - x) \cdot 1}{2}) = 1. \end{matrix}

Megjegyzés. A következő megoldás mutatja, hogy az ötszögre igazolt szabályosság a fentinél elegánsabban is felhasználható.

II. megoldás. Forgassuk el a

C D E

háromszöget a

C

pont körül úgy, hogy a

D

csúcs a

B

pontba kerüljön.

Az így kapott

C B E'

háromszög az

A B C

háromszöggel együtt éppen az

A C E'

háromszöget adja ki, ami egybevágó az

A C E

háromszöggel, hiszen az

A C

oldal közös mindkettőben,

C E = C E'

és

A E = 1 = A B + E D = A B + B E' = A E'

. Az ötszög területe tehát éppen kétszerese az

A C E'

háromszög területének. Mivel ebben a háromszögben az egység hosszúságú

A E'

oldalhoz tartozó

C B

magasság is egységnyi hosszú, a háromszög területe

\frac{1}{2}

, az ötszögé tehát éppen 1 területegység.

Megjegyzés. A megoldáshoz könnyen eljuthatunk az ötszögben rejlő szimmetria előzetes megsejtése nélkül is. Az

A C

és a

C E

szakaszok hossza a Pitagorasz-tétel szerint

A C = \sqrt[]{1 + x^{2}}

, illetve

C E = \sqrt[]{1 + {(1 - x)}^{2}} = \sqrt[]{2 - 2 x + x^{2}}

. Az

A C E

háromszög

C E

oldalára a koszinusz-tételt felírva:

\begin{matrix} 2 - 2 x + x^{2} = 1 + (1 + x^{2}) - 2 \cdot 1 \cdot \sqrt[]{1 + x^{2}} \cdot cos E A C ∢, \end{matrix}

ahonnan

cos E A C ∢ = \frac{x}{\sqrt[]{1 + x^{2}}} = cos B A C ∢

. Így, az ötszög konvexitása miatt

E A C ∢ = B A C ∢

, amiből következik, hogy az

A B C

háromszög egybevágó az

A P C

háromszöggel. Hasonlóan látható be a

C P E

és a

C D E

háromszögek egybevágósága is.