Kezdőlap


Feladat:	B.3745	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dányi Zsolt
Füzet:	2005/február, 94 - 96. oldal		PDF \| MathML
Témakör(ök):	Abszolútértékes egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2004/szeptember: B.3745

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Használjuk fel, hogy minden $t$ valós számra $| t | = | - t |$ , illetve hogy $| t | \geq t$ . Ezeket felhasználva az első feltételből $a + b > c - d$ , azaz

\begin{matrix} a + b + d > c, \end{matrix}

(1)

illetve

a + b > d - c

, azaz

\begin{matrix} a + b + c > d \end{matrix}

(2)

következik.
Hasonlóan kapjuk a második feltételből, hogy

c + d > a - b

és

c + d > b - a

, azaz

\begin{matrix} b + c + d & > a és & (3) \\ a + c + d & > b . & (4) \end{matrix}

(2)-ből kapjuk, hogy

b - d > - a - c

, (4)-ből pedig azt, hogy

b - d < a + c

. A két egyenlőtlenség együtt azt jelenti, hogy

a + c > b - d > - (a + c)

, tehát

| b - d | < a + c

II. megoldás. Az alábbi grafikus megoldásban a könnyebb követhetőség kedvéért a

b = x

és az

a = y

helyettesítéseket alkalmaztuk. A feltételek így az

\begin{matrix} x + y > | c - d |, \end{matrix}

(5)

illetve a

\begin{matrix} c + d > | y - x | \end{matrix}

(6)

alakot öltik, a bizonyítandó állítás pedig

\begin{matrix} y + c > | x - d | . \end{matrix}

(7)

(5) megoldáshalmaza egy nyílt félsík, melyet az

x + y = | c - d |

egyenletű

h

egyenes határol (1. ábra), a (6) egyenlőtlenség megoldáshalmaza pedig egy végtelen nyílt sáv, amelyet az

y = x - (c + d)

és az

y = x + (c + d)

egyenletű

h_{2}

és

h_{3}

egyenesek határolnak (2. ábra).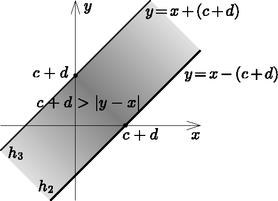

1. ábra.

x + y > | c - d |

2. ábra.

c + d > | y - x |

A két halmaz közös része egy ,,félsáv'', amelyet a 3. ábrán a koordinátarendszer nélkül ábrázolunk, hogy ne befolyásoljon

c

és

d

viszonya.

3. ábra

A feladat állítása szerint ez a halmaz része a (7) egyenlőtlenség megoldáshalmazának, amely egy nyílt negyedsík, az

y > | x |

jól ismert megoldáshalmazának eltoltja úgy, hogy a csúcs az origóból a

K (d; - c)

pontba kerül. A koordinátatengelyeket a 4. ábrán sem tüntettük fel.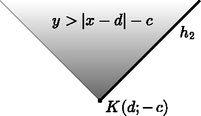

4. ábra.

y > | x - d | - c

Azt kell megmutatnunk, hogy a 4. ábra negyedsíkja a belsejében tartalmazza a 3. ábra félsávját: ha

(x; y)

-ra teljesül (5) és (6), akkor fennáll (7) is.
Vegyük észre, hogy a

K

pont rajta van a 2. ábra vastagon megrajzolt alsó határegyenesén,

K \in h_{2}

y_{K} = - c = x_{K} - (c + d) = d - c - d

. Másfelől a

K

koordinátáira

x_{K} + y_{K} = d - c ≯ | c - d |

, azért a

K

pont nincs az 1. ábra megoldáshalmazában; annak vagy a határán van (ha

d \geq c

), vagy pedig a külsejében (ha

d < c

). A 3. és 4. ábrák ponthalmazai tehát az 5a. vagy az 5b. ábrák szerint helyezkednek el.

5a. ábra.

d \geq c

5b. ábra.

d < c

Mivel a negyedsík a belsejében tartalmazza a nyílt félsávot, a feladat állítása valóban igaz.

Megjegyzések. 1. Mindkét bizonyításból kiderül, hogy az

a + c > | b - d |

egyenlőtlenség már az

a + b > d - c

és a

c + d > b - a

egyenlőtlenségekből is következik.
2. Érdekes geometriai jelentés adható a feladatban szereplő mennyiségeknek, ha

a

b

c

d

pozitív mennyiségek. Ebben az esetben ugyanis az

(| a - b |; c + d)

és a

(| c - d |; a + b)

intervallumok közös része nem üres, van tehát olyan

e

mennyiség, amelyre

| a - b | < e < a + b

és

| c - d | < e < c + d

, a háromszög-egyenlőtlenség szerint tehát létezik olyan négyszög, amelynek oldalai

a

b

c

d

, átlója pedig

e

(6. ábra).

6. ábra

A négyszög másik átlójára ekkor a háromszög-egyenlőtlenség szerint

a + c > f > | b - d |

, a bizonyítandó állítás.