Kezdőlap


Feladat:	B.3683	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Stippinger Marcell
Füzet:	2005/január, 31 - 33. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszögek geometriája, Sokszög lefedések, Feladat
Hivatkozás(ok):	Feladatok: 2003/december: B.3683

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás.
(1) Egy szabályos sokszög egy csúcsnál levő belső szöge $α = \frac{(n - 2) \cdot 180^{\circ}}{n}$ , ahol $n$ a sokszög csúcsainak száma. Tudjuk még, hogy $60^{\circ} \leq α < 180^{\circ}$ . Számoljuk ki ezt néhány szabályos sokszögre:

\begin{matrix} \begin{matrix} n & 3 & 4 & 5 & 6 & 7 & 8 \\ α & 60^{\circ} & 90^{\circ} & 108^{\circ} & 120^{\circ} & \approx 128, 571^{\circ} & 157, 5^{\circ} \end{matrix} \end{matrix}

A szabályos sokszögekben nagyobb csúcsszámhoz nagyobb belső szög tartozik.
Vizsgáljuk meg, hogy a lefedő szabályos sokszögek hogyan helyezkednek el a lefedendő sokszög oldalain. A lefedendő sokszög egy oldalának minden pontját le kell fedni, így az oldalon egymáshoz ,,nagyon közeli'' pontokat is. Nem fedhetünk le az oldalon minden pontot külön-külön sokszöggel, hiszen ekkor átfedés jönne létre. Ebből következik, hogy a lefedendő sokszög oldalán van két olyan pont, amelyeket ugyanaz a lefedő sokszög tartalmaz. A lefedő konvex sokszög viszont nem ,,lóghat le'' a lefedendőről (ezt írja elő a feladat az összerakás szóval), ezért egy oldala kell, hogy illeszkedjen a lefedendő sokszögre. Ez csak úgy lehetséges, ha megfelelő oldaluk egy egyenesbe esik. Mivel a lefedő és a lefedendő sokszög oldala egyenlő hosszú, azért ez ,,lelógás'' nélkül csak úgy lehetséges, ha az illeszkedő oldaluk végpontjai is egybeesnek.
Ebből következik, hogy a lefedendő sokszög csúcsainál lefedő sokszögek csúcsai találkoznak ‐ hiszen más sokszögekkel kell lefednünk, mint az eredeti. A képletből, illetve a táblázatból látszik, hogy kisebb belső szöge a kevesebb csúcsú sokszögnek van és ha nagyobb csúcsszámút használnánk a lefedéshez, akkor a területe nagyobb lenne a lefedendőnél, így nem lehet szó a feladatban kért összerakásról.
Látható, hogy a lefedendő sokszög belső szögeit a lefedő sokszögek belső szögeiből kell hézag és átfedés nélkül összerakni.
(2) Vizsgáljuk meg, hogy milyen szabályos sokszögeket illeszthetünk egymás mellé, hogy konvex szöget kapjunk:

‐

háromszög mellé:
‐ egy háromszöget:

60^{\circ} + 60^{\circ} = 120^{\circ}

; (I)
‐ egy négyzetet:

60^{\circ} + 90^{\circ} = 150^{\circ}

; (II)
‐ egy ötszöget:

60^{\circ} + 108^{\circ} = 168^{\circ}

; (III)
‐ egy hatszöget illesztve már egyenesszöget kapnánk, ami nem felel meg, mert kétszer akkora oldal jönne létre, mint a lefedendő sokszögé;
‐ nagyobb csúcsszámú sokszög esetén már konkáv szöget kapnánk.

‐	négyzet mellé: ‐ egy háromszöget (ezt már felsoroltuk); ‐ egy négyzetet illesztve már egyenesszöget kapnánk, ami nem felel meg; ‐ nagyobb csúcsszámú sokszög esetén konkáv szöget kapnánk.

‐	ötszög mellé: ‐ egy háromszöget (ezt már felsoroltuk); ‐ nagyobb csúcsszámú sokszög esetén konkáv szöget kapnánk;

‐

hat vagy nagyobb csúcsszámú sokszög mellé már a legkisebb belső szöggel rendelkező szabályos sokszöget (háromszöget) illesztve sem kaphatunk

180^{\circ}

-nál kisebb szöget. Ha pedig legalább három sokszög találkozna egy-egy csúcsban, akkor a lehetséges legkisebb szöget figyelembe véve is legalább

3 \cdot 60^{\circ} = 180^{\circ}

lenne a csúcsnál keletkező szögek összege, ami lehetetlen.

Most a fent kapott szögekről kell megvizsgálnunk, hogy melyik lehet szabályos sokszög belső szöge. Ezt a képletbe helyettesítve tesszük, úgy, hogy a csúcsok számát keressük, amelynek egész számnak kell lennie.

\begin{matrix} α = 120^{\circ} \Rightarrow 120^{\circ} = \frac{(n - 2) \cdot 180^{\circ}}{n} \Rightarrow 120 \cdot n = 180 \cdot n - 360 \Rightarrow n = 6. \end{matrix}

(I)

A szabályos hatszög valóban összerakható hat darab vele azonos oldalhosszúságú szabályos háromszögből.

\begin{matrix} α = 150^{\circ} \Rightarrow 150^{\circ} = \frac{(n - 2) \cdot 180^{\circ}}{n} \Rightarrow 150 \cdot n = 180 \cdot n - 360 \Rightarrow n = 12. \end{matrix}

(II)

A szabályos tizenkétszög valóban összerakható hat-hat darab felváltva illesztett azonos oldalhosszúságú szabályos háromszögből és négyzetből, középre pedig egy velük azonos oldalhosszúságú szabályos hatszöget kell helyezni.

\begin{matrix} α = 168^{\circ} \Rightarrow 168^{\circ} = \frac{(n - 2) \cdot 180^{\circ}}{n} \Rightarrow 168 \cdot n = 180 \cdot n - 360 \Rightarrow n = 30. \end{matrix}

(III)

Ha a szabályos 30-szög oldalaira befelé felváltva rajzolunk szabályos öt- és háromszögeket, akkor a 30-szög belsejében

360^{\circ} - 108^{\circ} - 60^{\circ} - 108^{\circ} = 84^{\circ}

-os szög keletkezik (lásd ábra), ami nem belső szöge egyetlen szabályos sokszögnek sem, és a (2) felsorolás alapján sem áll elő szabályos sokszögek belső szögeinek összegeként.
Az (I) és (II) eset megvalósítható, lásd az

(a)

és

(b)

ábrákat. A megfelelő lefedő sokszögek egymás mellé kerülő szögei kiadják a lefedendő sokszög belső szögeit, illetve ha a lefedendő sokszög belsejében vannak, akkor a teljesszöget, átfedés pedig nem jön létre. A lefedő és a lefedendő sokszögek oldalainak hossza egyenlő.

(a)

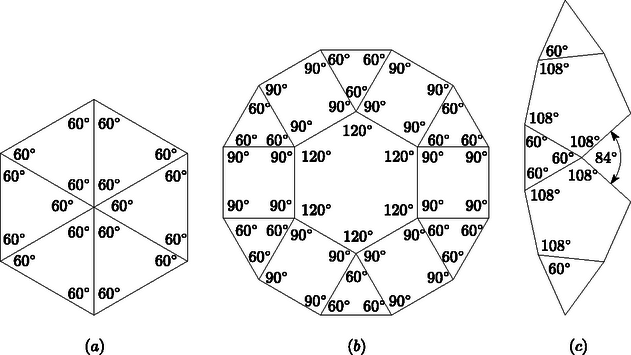szabályos hatszög;

(b)

szabályos tizenkétszög,

(c)

szabályos

30

-szög kerületének egy részlete; a

84^{\circ}

-os szög nem állítható elő a feladat feltételeinek megfelelően