Feladat: A.344 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Puskás Anna ,  Torma Róbert 
Füzet: 2005/május, 281 - 283. oldal  PDF  |  MathML 
Témakör(ök): Sík parkettázás, Nehéz feladat
Hivatkozás(ok):Feladatok: 2004/április: A.344

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. megoldás. Megmutatjuk, hogy ilyen téglalap nem létezik. Tételezzük fel, hogy létezik olyan rácstéglalap, amely kicsempézhető, és vegyük ennek egy tetszőleges csempézését.
Minden egyes csempében kössük össze a két 2 hosszúságú oldal felezőpontját egy görbével az 1. ábra szerint; a görbe legyen merőleges a végpontjaiban a két oldalra. Mivel a 2 hosszúságú oldalakhoz egy-egy újabb csempe illeszkedik, a görbedarabok egymáshoz csatlakoznak és zárt hurkokat alkotnak.

 
 

1. ábra
 

Vegyük az egyik zárt hurkot. Rajzoljunk a hurkot alkotó görbedarabokra egy-egy nyilat a pozitív körüljárás irányában (2. ábra). A csempéket két csoportra oszthatjuk: az egyik fajta csempében a görbe ,,befelé kanyarodik''; az iránya pozitív irányban változik 90∘-ot, a csempék másik csoportjában a görbe ,,kifelé kanyarodik'', az irány negatív irányban változik 90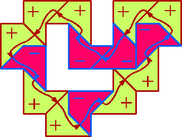∘-ot.
 
 

2. ábra
 

Legyen a kifelé kanyarodó görbedarabok száma k. Mivel a görbe iránya összesen 360∘-ot változik pozitív irányban, a befelé kanyarodó szakaszok száma k+4.
Cseréljük most ki a görbedarabokat egyenes szakaszokra, és vizsgáljuk meg, hogy az így kapott töröttvonal belsejének mekkora lehet a területe, és ebből mennyit fedhetnek le a csempék (3. ábra). A töröttvonal belseje felbontható 2 oldalú, átlós helyzetű négyzetekre. Mindegyik ilyen négyzet területe 2, a töröttvonal által bekerített terület tehát páros egész szám.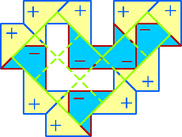
 
 

3. ábra
 

A befelé kanyarodó csempék területéből 14 egység esik a töröttvonal belső oldalára, a kifelé kanyarodó csempék területéből pedig 74 egység. Lehetnek olyan csempék is, amelyek teljes egészükben a töröttvonal belsejébe esnek; legyen az ilyen csempék száma b. Ezek mindegyike 2‐2 egységnyi területet fed le. Az összes lefedett terület tehát
(k+4)⋅14+k⋅74+b⋅2=2k+2b+1,
ami páratlan. A töröttvonal által határolt páros mérőszámú területből tehát a csempék egy páratlan méretű részt fednek le, tehát nem fedhetik le teljesen.
 
II. megoldás. A megoldáshoz szükségünk lesz a következő segédtételre:
 

Ha az egyszerű, zárt T töröttvonal csak vízszintes és függőleges rácsszakaszokból áll, és a belsejében nincs rácspont, akkor a T által határolt négyzetek között mindig van olyan, amelynek legalább három oldala T-hez tartozik.
 

Bizonyítás. Tekintsük azt a gráfot, amelynek csúcsai a T által határolt négyzetek, és kössük össze éllel a szomszédos négyzetekhez tartozó csúcsokat (4. ábra). Ez a gráf összefüggő, és nem tartalmazhat kört, mert ha néhány négyzet egy kört alkotna, akkor ennek belsejében lenne olyan rácspont, amelyen T nem megy át. A gráf tehát egy fa. Egy fában mindig van elsőfokú pont. Ha pedig a gráfunk valamelyik pontja legfeljebb elsőfokú, az azt jelenti, hogy a megfelelő négyzetnek legfeljebb csak egy oldalához csatlakozik további négyzet, legalább három oldala pedig T-nek is oldala. Ezzel a segédtételt igazoltuk.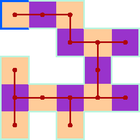
 
 

4. ábra
 

Most tételezzük fel, hogy sikerült a megadott mintával egy téglalapot kicsempézni. Kössük össze ismét mindegyik csempében a 2 hosszú oldalak felezőpontjait egy-egy szakasszal. Ezek a szakaszok zárt töröttvonalakat alkotnak, amelyeknek nincs közös pontjuk; két töröttvonal vagy egymáson kívül helyezkedik el, vagy egyikük a belsejében tartalmazza a másikat.
A legkisebb területű töröttvonal nem tartalmazhat a belsejében további töröttvonalat. A belsejét azok a csempék fedik le, amelyek a töröttvonalat alkotják. A továbbiakban megmutatjuk, hogy ez nem lehetséges. Tegyük fel tehát, hogy létezik a csempéknek egy olyan elrendezése, amelyben a csempékre rajzolt szakaszok egyetlen zárt töröttvonalat alkotnak, és ennek a vonalnak a belsejét a felhasznált csempék teljesen lefedik. Tekintsünk az ilyen elrendezések közül egy olyat, amelyikben a felhasznált csempék száma minimális.
A töröttvonalat alkotó, 2 hosszúságú szakaszok egy átlós helyzetű négyzetrács élei mentén haladnak úgy, hogy a töröttvonal belsejében nem maradhat ki rácspont. (Minden bekerített rácspont lefedetlen területet jelentene.) A segédtétel szerint van közöttük három, egymáshoz merőlegesen csatlakozó úgy, hogy az általuk közrefogott négyzet a töröttvonal belsejébe esik. Válasszunk ki három ilyen szakaszt, az ezeket tartalmazó és a szomszédos rácsnégyzeteket pedig betűzzük meg az 5. ábra szerint.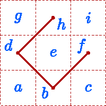
 
 

5. ábra
 

A b, d, f, h mezőket a csempék határai átlósan kettéosztják úgy, hogy a csúcsban szomszédos mezők ellentétes irányban vannak felosztva. A szimmetria miatt feltételezhetjük, hogy ez a 6. ábrán látható irányokban történik.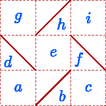
 
 

6. ábra
 

Vizsgáljuk most meg, hogy a bd, bf és dh szakaszok milyen csempékhez tartozhatnak. A bd csempe mindenképpen tartalmazza a b mező bal-felső felét. Ezért a bf csempe a b mezőnek csak a jobb-alsó felét tartalmazhatja, ez a csempe tehát a b mező jobb-alsó feléből, a c mezőből és az f mező bal-alsó feléből áll. Hasonlóan, a dh csempe tartalmazza a d mező jobb-felső felét, ezért a bd csempe a d mező bal-alsó feléből, az a mezőből és a b mező bal-felső feléből áll. Az e mezőt lefedő csempe ezek után csak a d mező jobb-felső és a h mező jobb-alsó felét tartalmazhatja (7. ábra).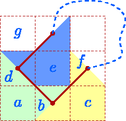
 
 

7. ábra
 

Módosítsuk a csempézéseket a következőképpen. Hagyjuk el a bd, bf és dh csempéket, és illesszünk be helyettük egy újat a 8. ábra szerint az e, f, h mezőkre. Ezáltal a csempék száma csökken, és a módosított hurok belsejét továbbra is lefedik a csempék. Találtunk tehát egy még kisebb csemperendszert, amely egyetlen hurokból áll, és amelynek belsejét a csempék lefedik. Ez pedig ellentmond annak, hogy a minimális hurokból indultunk ki. A megadott mintával tehát valóban nem lehet rácstéglalapot kicsempézni.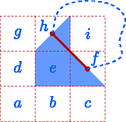
 
 

8. ábra