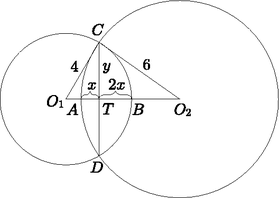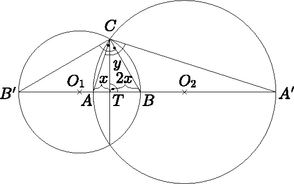Kezdőlap


Feladat:	B.3722	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Cseh Ágnes
Füzet:	2005/április, 216. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Thalesz tétel és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 2004/április: B.3722

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Használjuk az 1. ábra jelöléseit. Legyen $A T = x$ (így $B T = 2 x$ lesz) és $T C = y$ . Az $O_{1} T C$ és az $O_{2} T C$ háromszög derékszögű, felírható oldalaikra a Pitagorasz-tétel:

\begin{matrix} {(4 - 2 x)}^{2} + y^{2} & = 4^{2}, & {(6 - x)}^{2} + y^{2} & = 6^{2}, \\ 16 - 16 x + 4 x^{2} + y^{2} & = 16, & 36 - 12 x + x^{2} + y^{2} & = 36, \\ 4 x^{2} + y^{2} & = 16 x, & x^{2} + y^{2} & = 12 x . \end{matrix}

Ebből

4 x^{2} + y^{2} = x^{2} + y^{2} + 4 x

3 x^{2} = 4 x

. (Itt

x = 0

esetén nem metszené, hanem érintené egymást a két kör, tehát

x \neq 0

.) Tehát

x = \frac{4}{3}

, ahonnan

\begin{matrix} O_{1} O_{2} = 4 + 6 - 3 x = 6 (cm) . \end{matrix}

A körök középpontjának távolsága 6 cm (ami azt jelenti, hogy a kisebbik kör középpontja éppen illeszkedik a nagyobb körre).

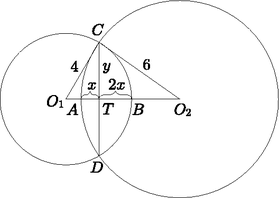1. ábra

II. megoldás. Használjuk az I. megoldás jelöléseit (2. ábra). Az

O_{1} O_{2}

egyenesének az

O_{2}

középpontú körrel vett másik metszéspontja legyen

A'

, az

O_{1}

középpontú körrel vett másik metszéspontja pedig legyen

B'

. Thalész tétele szerint a

B C B'

háromszög és az

A' C A

háromszög derékszögű, és mindkettőnek

C T

az átfogóhoz tartozó magassága. Alkalmazzuk rájuk a magasságtételt:

\begin{matrix} B' T \cdot B T = T C^{2} és A' T \cdot A T = T C^{2}, azaz B' T \cdot B T = A' T \cdot A T . \end{matrix}

(8 - 2 x) \cdot 2 x = (12 - x) \cdot x

, ahol

x \neq 0

, különben érintenék egymást a körök. Tehát

(8 - 2 x) \cdot 2 = 12 - x

, ahonnan

x = \frac{4}{3}

, így

O_{1} O_{2} = 6

(cm).

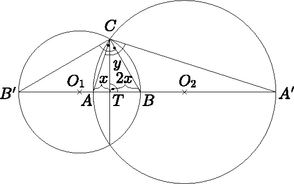2. ábra