Kezdőlap


Feladat:	B.3714	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bereczki Péter , Bogár Péter , Cserép Gergely , Estélyi István , Gehér György , Gidófalvy Kitti , Győrffy Balázs , Haszpra Tímea , Jankó Zsuzsanna , Kórus Péter , Kovács Péter , Kunovszki Péter , Kurgis Zsuzsanna , Lorántffy Bettina , Majoros Csilla , Nagy Csaba , Nagy-Baló András , Nándori Péter , Nikházy László , Pálovics Róbert , Papp Márton , Petényi Franciska , Poronyi Balázs , Stippinger Marcell , Sümegi Károly , Udvari Balázs , Ureczky Bálint
Füzet:	2005/március, 156 - 157. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai szerkesztések, Háromszög-egyenlőtlenség alkalmazásai, Szinusztétel alkalmazása, Párhuzamos szelők tétele és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 2004/március: B.3714

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Ha adott a háromszög $K$ kerülete és a $c$ oldala, akkor ezzel adottnak vehető másik két oldalának összege, $a + b$ is. Hosszabbítsuk meg a $B C$ oldalt $C$ -n túl és mérjük fel rá a $b$ -t. Így az $A B D$ háromszöget kapjuk. Az $A C D$ háromszög két oldala $b$ , ezért egyenlő szárú és mivel a szárszög melletti külső szöge $γ$ , azért

\begin{matrix} D A C ∢ = A D C ∢ = \frac{γ}{2} . \end{matrix}

A szerkesztés menete: Felvesszük a

B D = a + b

szakaszt és

D

-ben rámásoljuk a

γ

szög felét.

B

köré

c

sugarú kört szerkesztünk. Ahol metszi a

\frac{γ}{2}

szög másik szárát, ott van az

A

pont. Az

A D

szakasz felezőmerőlegese és

D B

metszéspontja

C

.
Diszkusszió: A megoldhatóságnak nyilván feltétele, hogy a kerület legyen nagyobb a

c

oldalnál és

γ < 180^{\circ}

. A háromszög-egyenlőtlenség miatt szükséges, hogy

a + b > c

teljesüljön, vagyis a kerület legyen nagyobb a

c

kétszeresénél.
Az

A B D

háromszögben adott két oldal és a kisebbikkel szemközti szög. Legyen

D A B ∢ = δ

. A szinusz-tétel miatt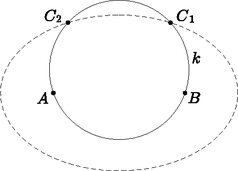

\begin{matrix} sin δ = \frac{(a + b) sin \frac{γ}{2}}{c} . \end{matrix}

(Itt

(a + b) = K - c

, tehát

sin δ

értéke csak a megadott adatoktól függ.) Ha ez az érték nagyobb, mint 1, akkor nincs megoldás; ha egyenlő 1-gyel, akkor egy megoldás van; és ha kisebb, mint 1, akkor két egybevágó megoldás van (ld. 2. megjegyzés).

Megjegyzések. 1. Ha másképpen indulunk el, akkor egyszerűbb a megoldás szerkezete. A szinusztétel szerint

\begin{matrix} 2 R = \frac{c}{sin γ}, \end{matrix}

tehát az

A B C

háromszög

k

körülírt köre megszerkeszthető. A

C

csúcs így rajta van a

k

körön, másfelől

C A + C B = a + b

miatt az

A

B

fókuszú,

(a + b)

nagytengelyű ellipszisen¹. A kör és az ellipszis metszéspontjai a szimmetrikus elrendezés miatt most egyszerűen megszerkeszthetők.

2. Az ábra szimmetriájának nyilvánvaló következménye, hogy ha van megoldása a feladatnak, akkor az így egyértelműen meghatározott, mivel

A B C_{1}

és

A B C_{2}

tükrösek. A közölt megoldás záróközleménye szerint ebben az esetben ,,két egybevágó megoldás van''.
Valóban, a

B

középpontú,

c

sugarú kör az

A_{1}

és

A_{2}

pontokban metszi a

D

-ből induló, a

D B

-vel

\frac{γ}{2}

szöget bezáró félegyenest. Az ábra jelölései szerint legyen

B A_{1} A_{2} ∢ = B A_{2} A_{1} ∢ = δ

. Mivel

B D A_{2} ∢ = H A_{2} D ∢ = \frac{γ}{2}

, azért

B H A_{2} ∢ = γ

. Így az

A_{1} B C

és az

A_{2} B H

háromszögek egy oldala (

c

) és ezzel szemközti szöge (

γ

) megegyezik, de még egy szögük egyenlő, mert: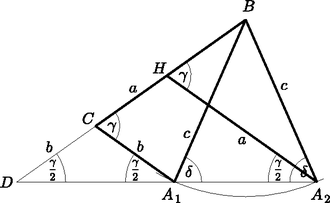

\begin{matrix} D A_{1} C ∢ + C A_{1} B ∢ + B A_{1} A_{2} ∢ & = 180^{\circ} = B C A_{1} ∢ + C A_{1} B ∢ + A_{1} B C ∢, \\ \frac{γ}{2} + δ & = γ + A_{1} B C ∢, \end{matrix}

amiből

A_{1} B C ∢ = δ - \frac{γ}{2}

. A

B A_{2} H

szög is

δ - \frac{γ}{2}

-vel egyenlő, ezért

A_{1} B C ∢ = B A_{2} H ∢

Az egybevágóság egy másik bizonyítása látható a borítón: A

D A_{1} C

D A_{2} H

és az

A_{1} A_{2} B

egyenlő szárú háromszögek alapjainak felezőpontja legyen rendre

E

F

és

G

. Ekkor:

\begin{matrix} \bar{D E} = \frac{\bar{D A_{1}}}{2} és \bar{F G} = \frac{\bar{D A_{1}} + \bar{A_{1} A_{2}}}{2} - \frac{\bar{A_{1} A_{2}}}{2} = \frac{\bar{D A_{1}}}{2}, \end{matrix}

tehát

D E = F G

. A párhuzamos szelők tételéből következik, hogy

D C = H B = b

. Így

C B = D B - D C = (a + b) - b = a

. Hasonlóan

D H = a

. Tehát a

C A_{1} B

és a

H B A_{2}

háromszögek mindhárom oldala megegyezik, ezért a két háromszög egybevágó.

¹Ld. Kiss György: Amit jó tudni a kúpszeletekről I‐II., KöMaL 2004/8. sz., 450. oldal, 2004/9. sz., 514. oldal; illetve honlapunkon (www.komal.hu).