Kezdőlap


Feladat:	2003. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	2004/február, 67 - 69. oldal		PDF \| MathML
Témakör(ök):	Pont körre vonatkozó hatványa, Síkgeometriai számítások trigonometriával, Síkgeometriai bizonyítások, Thalesz tétel és megfordítása, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 2004/február: 2003. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B F$ háromszög köré írt $k_{1}$ kör és az $E F$ egyenes $F$ -től különböző metszéspontja $G$ . Az $E$ pontnak $k_{1}$ körre vonatkozó hatványa $A E \cdot E B = F E \cdot E G$ állandó, ezért a $G$ pont helyzete nem függ az $A$ , $B$ pontpár megválasztásától.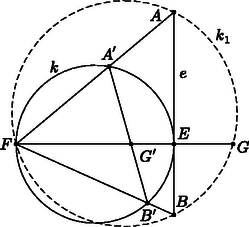

Tekintsük most azt az inverziót, amelynek alapköre az

F

középpontú,

E F

sugarú kör. Az

e

egyenes inverze a

k

kör, az

A

és

B

pontok inverze az

A'

, illetve a

B'

pont. A

k_{1}

kör inverze az

A' B'

egyenes; ezen belül is a

G

-t tartalmazó körív képe az

A' B'

szakasz. Az

A' B'

szakasz tehát mindig átmegy a

G

pont inverzén,

G'

-n, mely, mint azt láttuk, független az

A

és

B

pontok választásától.

□

Megjegyzések. 1. A fenti megoldás az inverzió tulajdonságaira épít, amely nem feltétlenül tananyag a középiskolában (lásd hátsó belső borítóoldalt). Ugyancsak inverziót használ megoldásában Balogh László és Maga Péter.
2. A fenti megoldásból könnyen látható, hogy ha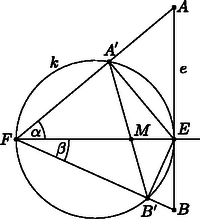

E F = 1

, akkor

\begin{matrix} F G' = \frac{1}{F G} = \frac{1}{1 + E G} = \frac{1}{1 + A E \cdot E B} . \end{matrix}

A továbbiakban megadunk két, szokásosabb megoldást is.

II. megoldás. Legyen most

E F

és

A' B'

metszéspontja

M

. Megmutatjuk, hogy

M

minden

A

B

pár esetén ugyanaz a pont; másképpen, az

F M

hossza állandó. Az

F M

hosszát az

F A' B'

háromszög és

F A' E B'

négyszög területének arányával fogjuk kifejezni:

\begin{matrix} \frac{F M}{E F} = \frac{t_{F A' B'}}{t_{F A' E B'}} . \end{matrix}

Válasszuk az

E F

szakasz hosszát egységnek, legyen

A F E ∢ = α

és

B F E ∢ = β

. Az érintő tulajdonság és a Thalész-tétel szerint az

F E A

F E B

, illetve

F A' E

és

F B' E

háromszögek derékszögűek, így

A E = tan α

B E = tan β

F A' = cos α

F B' = cos β

A' E = sin α

és

B' E = sin β

. A keresett területek tehát:

\begin{matrix} t_{F A' B'} & = & \frac{1}{2} F A' \cdot F B' sin (α + β) = \frac{cos α \cdot cos β \cdot sin (α + β)}{2} \\ t_{F A' E B'} & = & t_{F A' E} + t_{F E B'} = \frac{sin α cos α + sin β cos β}{2} = \frac{sin 2 α + sin 2 β}{4} = \\ = & \frac{sin (α + β) cos (α - β)}{2} . \end{matrix}

Végül

\begin{matrix} F M & = & \frac{F M}{E F} = \frac{t_{F A' B'}}{t_{F A' E B'}} = \frac{cos α cos β}{cos (α - β)} = \frac{cos α cos β}{cos α cos β - sin α sin β} = \\ = & \frac{1}{1 + tan α tan β} = \frac{1}{1 + E A \cdot E B} \end{matrix}

F M

szakasz hossza tehát állandó.

□

III. megoldásvázlat (Kis Gergely megoldása). Válasszuk

k

középpontját az origónak, sugarát egységnyinek, legyenek továbbá az

A

és

B

pontok koordinátái rendre

(1; a)

, ill.

(1; b)

. Az

A F

és

B F

egyenesek, ill. a

k

kör egyenletei rendre

\begin{matrix} \frac{a x}{2} + \frac{a}{2} & = & y \\ \frac{b x}{2} + \frac{b}{2} & = & y \\ x^{2} + y^{2} & = & 1 \end{matrix}

A megfelelő egyenletpárok megoldásából a metszéspontokra

\begin{matrix} A' = (\frac{8}{a^{2} + 4} - 1; \frac{4 a}{a^{2} + 4}) és B' = (\frac{8}{b^{2} + 4} - 1; \frac{4 b}{b^{2} + 4}) \end{matrix}

adódik. Az

A' B'

egyenes egyenlete innen

\begin{matrix} \frac{4 + a b}{2 (a + b)} (x + 1 - \frac{8}{a^{2} + 4}) + \frac{4 a}{a^{2} + 4} = y . \end{matrix}

A' B'

egyenes

x

tengellyel való metszéspontjának

x

koordinátája a fenti egyenletből

y = 0

helyettesítéssel

\begin{matrix} x_{0} = \frac{4 + a b}{4 - a b} . \end{matrix}

Ez a mennyiség állandó, hiszen

a b

állandó. Ez azt jelenti, hogy az

A' B'

egyenesek mindegyike átmegy az

(x_{0}; 0)

ponton.

□