Feladat: B.3611 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 2004/április, 222 - 223. oldal  PDF  |  MathML 
Témakör(ök): Rekurzív sorozatok, Feladat
Hivatkozás(ok):Feladatok: 2003/január: B.3611

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A sorozat az xn+1=f(xn) rekurzióval van megadva, ahol f(x)=x2-x+1. Az f függvény grafikonja az ábrán látható, megrajzoltuk az y=x egyenletű egyenest is, amely a görbét az (1;1) pontban érinti. A grafikonról látható, hogy f(x)≥34, tehát ha x1≠0, akkor az 1xi sorozat minden tagja értelmes.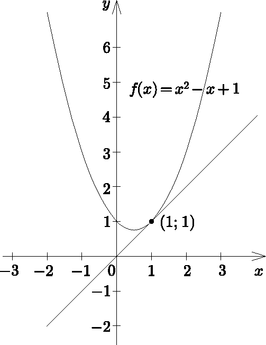

 
 

Ha 0<x<1, akkor 0<x<f(x)<1, tehát ha x1, a sorozat első tagja 0 és 1 közé esik, mint a feladat a) részében, akkor az 1xi sorozat minden tagja nagyobb 1-nél, a ∑i=1∞1xi végtelen sor tehát divergens.
Az adott rekurziót átrendezve kapjuk, hogy
xn+1-1=xn(xn-1)
és mivel f(x)=1 pontosan akkor teljesül, ha x=0 vagy x=1, a fenti egyenlőségben nullától különböző értékek állnak, ha a sorozat első tagja nem 0 vagy 1. Mindkét oldal reciprokát véve:
1xn+1-1=1xn(xn-1).
Vegyük észre, hogy a jobb oldal különbségként írható: 1xn(xn-1)=1xn-1-1xn és így
1xn+1-1=1xn-1-1xn,
amit átrendezve a rendkívül jól kezelhető ,,teleszkopikus'' különbséghez jutunk:
1xn=1xn-1-1xn+1-1.
Innen ugyanis a vizsgált sor n-edik részletösszege:
Sn=∑i=1n1xi=(1x1-1-1x2-1)+(1x2-1-1x3-1)+...++(1xn-1-1xn+1-1)=1x1-1-1xn+1-1.
Ha x>1, akkor nyilván 1<x<f(x), tehát az xn sorozat szigorúan monoton növő. Az xi+1-xi=(xi-1)2 egyenlőségeket összeadva:
xn+1-x1=(xn+1-xn)+(xn-xn-1)+⋯+(x2-x1)==(xn-1)2+(xn-1-1)2+⋯+(x1-1)2>n(x1-1)2,
tehát az xn sorozat végtelenhez tart és így az 1xn+1-1 sorozat határértéke nulla.
Az Sn sorozat határértéke tehát x1>1 esetén 1x1-1, vagyis ha x1=2, akkor a ∑i=1∞1xi végtelen sor összege 1.
 
Megjegyzések. 1. Ha x1<0, akkor a sorozat második tagja 1-nél nagyobb és így a fentiek szerint ebben az esetben is 1x1-1 a ∑i=1∞1xi végtelen sor összege.
2. Könnyen igazolható, hogy ha x1 nem 0 vagy 1, akkor (x1-1)∑i=1n1xi+∏i=1n1xi=1. A feladat kérdéseire ennek az azonosságnak a felhasználásával is gyors válasz adható.
3. Abban az esetben, ha x1=2, az xn sorozatnak érdekes tulajdonságai vannak. Először is könnyen igazolható, hogy ebben az esetben az xn+1=1+x1x2⋯xn rekurzió számolja ki a sorozat elemeit: x1=2, x2=3, x3=7, x4=43, ..., másrészt erre a sorozatra teljesül a következő állítás: ha n darab pozitív egész szám reciprokának összege kisebb 1-nél, akkor ez az összeg legfeljebb 1x1+1x2+⋯+1xn. Ha belegondol az ember, már az sem nyilvánvaló, hogy az 1-nél kisebb értékű n-tagú reciprokösszegek között egyáltalán létezik legnagyobb...