Kezdőlap


Feladat:	B.3608	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2004/március, 143 - 148. oldal		PDF \| MathML
Témakör(ök):	Harmadfokú (és arra visszavezethető) egyenletek, Gyökök és együtthatók közötti összefüggések, Feladat
Hivatkozás(ok):	Feladatok: 2003/január: B.3608

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Ha $x_{1}$ , $x_{2}$ , $x_{3}$ jelöli az

\begin{matrix} x^{3} - 3 x + 1 = 0 \end{matrix}

(1)

egyenlet gyökeit, akkor a Vite-formulák szerint

\begin{matrix} x_{1} + x_{2} + x_{3} = 0, x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} = - 3 és x_{1} x_{2} x_{3} = - 1. \end{matrix}

Hasonlóan kapjuk, hogy a keresett

a

b

c

számokra fenn kell állnia a

\begin{matrix} - a = x_{1}^{5} + x_{2}^{5} + x_{3}^{5}, b = x_{1}^{5} x_{2}^{5} + x_{2}^{5} x_{3}^{5} + x_{3}^{5} x_{1}^{5}, - c = x_{1}^{5} x_{2}^{5} x_{3}^{5} \end{matrix}

összefüggéseknek.
Elvben világos a teendőnk: a három egyenlet jobb oldalán az

x_{1}

x_{2}

x_{3}

változók szimmetrikus polinomjai állnak, ezek pedig a szimmetrikus polinomok alaptétele szerint kifejezhetők a változók elemi szimmetrikus polinomjaival, tehát (1) együtthatóival. Bár

c

értéke nyomban adódik,

a

és

b

meghatározása meglehetősen hosszadalmas számolásnak ígérkezik. A megoldók többsége ezt sikeresen elvégezte. Ehhez nem is kell ismerni a megoldás hátterében lévő tételt. Az alábbiakban két gyorsabb megoldást mutatunk, az egyik a fenti hatványösszegeket határozza meg célratörőbben és igen áttekinthető módon, a másik pedig közvetlenül a keresett polinomot írja fel.

I. megoldás. A gyökök ötödik hatványösszegének gyorsabb kiszámolásához a polinomok körében elvégezhető maradékos osztási eljárásnak egy nyilvánvaló, de rendkívül hasznos következményét használjuk fel.

α

gyöke a

g (x)

polinomnak és az

f (x)

polinomot a

g (x)

-szel maradékosan elosztva a maradék

r (x)

, akkor

f (α) = r (α)

, tehát az osztandó és a maradék azonos értékeket vesznek föl az osztó gyökein.

Az állítás nyomban adódik, ha az

f (x) = g (x) \cdot q (x) + r (x)

egyenlőségben a változó helyére

α

-t helyettesítünk, hiszen

g (α)

a feltétel szerint nulla. Eredményünk másképpen azt jelenti, hogy az

α

minden

f (α)

polinomja egy

g

-nél alacsonyabb fokszámú polinom, a

g

-vel való osztási maradék helyettesítési értékeként számolható.
Legyen tehát

g (x) = x^{3} - 3 x + 1

. Ekkor

g (x)

gyökeinek ötödik hatványát kell kiszámolnunk, az

f (x) = x^{5}

polinom helyettesítési értékét az

x_{1}

x_{2}

x_{3}

helyeken, pontosabban ezek összegét. Osszuk el maradékosan az

f (x)

polinomot a

g (x)

-szel:

\begin{matrix} x^{5} = (x^{3} - 3 x + 1) (x^{2} + 3) - x^{2} + 9 x - 3, \end{matrix}

r (x)

maradék

- x^{2} + 9 x - 3

. A fentiek szerint ekkor

x_{i}^{5} = - x_{i}^{2} + 9 x_{i} - 3

. Innen pedig

x_{1}^{5} + x_{2}^{5} + x_{3}^{5} = - (x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) + 9 (x_{1} + x_{2} + x_{3}) - 3 \cdot 3

, a tényleges feladat tehát a gyökök négyzetösszegének a meghatározása, amely az ismert módon

\begin{matrix} x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = ({\underset{︸}{x_{1} + x_{2} + x_{3}}}_{0}^{})^{2} - 2 ({\underset{︸}{x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1}}}_{- 3}^{}) . \end{matrix}

Minden szereplő kifejezés értékét ismerjük, így

\begin{matrix} - a = x_{1}^{5} + x_{2}^{5} + x_{3}^{5} = - (x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) + 9 (x_{1} + x_{2} + x_{3}) - 3 \cdot 3 = - 6 - 9 = - 15. \end{matrix}

b

kiszámolásához gondoljuk meg, milyen ,,könnyen'' ment a gyökök ötödik hatványösszegének a meghatározása. Ezért aztán ahelyett, hogy általában bajlódnánk az ötödik hatványok kéttényezős szorzatainak az összegével, jobb vásárnak tűnik, ha elkészítünk egy olyan

g (x)

harmadfokú polinomot, amelynek a gyökei éppen ezek a kéttényezős szorzatok,

x_{1} x_{2}

x_{2} x_{3}

, illetve

x_{3} x_{1}

. Az így kapott polinom gyökeinek ötödik hatványösszegét azután már gyorsan számolhatjuk a fenti módszerrel, a maradékos osztás után már ,,csak'' ezeknek a kéttényezős szorzatoknak a négyzetösszegére van szükségünk.
Megint a Vite-formulákat felhasználva

g (x) = x^{3} - b_{1} x^{2} + b_{2} x - b_{3}

, ahol

\begin{matrix} b_{1} & = x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} = - 3, \\ b_{2} & = x_{1} x_{2}^{2} x_{3} + x_{2} x_{3}^{2} x_{1} + x_{3} x_{1}^{2} x_{2} = x_{1} x_{2} x_{3} (x_{1} + x_{2} + x_{3}) = 0, végül \\ b_{3} & = x_{1} x_{2} x_{2} x_{3} x_{3} x_{1} = {(x_{1} x_{2} x_{3})}^{2} = 1, \end{matrix}

tehát most

g (x) = x^{3} + 3 x^{2} - 1

. Elvégezve a maradékos osztást

\begin{matrix} x^{5} = (x^{3} + 3 x^{2} - 1) (x^{2} - 3 x + 9) - 26 x^{2} - 3 x + 9. \end{matrix}

A fenti eljárást szó szerint megismételve

\begin{matrix} x_{1}^{5} x_{2}^{5} + x_{2}^{5} x_{3}^{5} + x_{3}^{5} x_{1}^{5} = - 26 (x_{1}^{2} x_{2}^{2} + x_{2}^{2} x_{3}^{2} + x_{3}^{2} x_{1}^{2}) - 3 (x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1}) + 3 \cdot 9. \end{matrix}

Mivel

x_{1}^{2} x_{2}^{2} + x_{2}^{2} x_{3}^{2} + x_{3}^{2} x_{1}^{2} = b_{1}^{2} - 2 b_{2} = 9

, az eredmény nyomban adódik:

\begin{matrix} b = x_{1}^{5} x_{2}^{5} + x_{2}^{5} x_{3}^{5} + x_{3}^{5} x_{1}^{5} = - 26 \cdot 9 + 9 + 3 \cdot 9 = - 198. \end{matrix}

A keresett polinom tehát

x^{3} + 15 x^{2} - 198 x + 1

Megjegyzés. A megoldás módszerével általánosan is megoldható a feladat: ha

x_{1}

x_{2}

x_{3}

g_{1} (x) = x^{3} - a_{1} x^{2} + a_{2} x - a_{3}

polinom gyökei, azaz

\begin{matrix} a_{1} = x_{1} + x_{2} + x_{3}, a_{2} = x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1}, a_{3} = x_{1} x_{2} x_{3}, \end{matrix}

akkor a

q_{1} = x_{1}^{5} + x_{2}^{5} + x_{3}^{5}

q_{2} = x_{1}^{5} x_{2}^{5} + x_{2}^{5} x_{3}^{5} + x_{3}^{5} x_{1}^{5}

q_{3} = x_{1}^{5} x_{2}^{5} x_{3}^{5}

mennyiségek a következőképpen számolhatók:

q_{3}

értéke közvetlenül adódik,

q_{3} = {(x_{1} x_{2} x_{3})}^{5} = a_{3}^{5}

q_{1}

kiszámításához az

f (x) = x^{5}

polinomot kell maradékosan elosztani a

g_{1} (x) = x^{3} - a_{1} x^{2} + a_{2} x - a_{3}

polinommal. Ezt elvégezve kapjuk, hogy a maradék

\begin{matrix} r (x) = (a_{1}^{3} - 2 a_{2} a_{1} + a_{3}) x^{2} + (a_{2}^{2} - a_{1}^{2} a_{2} + a_{1} a_{3}) x + (a_{1}^{2} - a_{2}) a_{3} . \end{matrix}

Innen pedig

\begin{matrix} q_{1} & = & r (x_{1}) + r (x_{2}) + r (x_{3}) = (a_{1}^{3} - 2 a_{2} a_{1} + a_{3}) (x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) + \\ + (a_{2}^{2} - a_{1}^{2} a_{2} + a_{1} a_{3}) (x_{1} + x_{2} + x_{3}) + 3 \cdot (a_{1}^{2} - a_{2}) a_{3} . \end{matrix}

Felhasználva, hogy a gyökök négyzetösszege

x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = a_{1}^{2} - 2 a_{2}

, megvan az eredmény:

\begin{matrix} q_{1} = (a_{1}^{3} - 2 a_{2} a_{1} + a_{3}) (a_{1}^{2} - 2 a_{2}) + (a_{2}^{2} - a_{1}^{2} a_{2} + a_{1} a_{3}) a_{1} + 3 \cdot (a_{1}^{2} - a_{2}) a_{3}, \end{matrix}

ami ,,puszta kézzel'' elég barátságtalan számolás volna. Áttekinthetőbb alakot kapunk egyébként, ha az

a_{1}

hatványai szerint rendezve is felírjuk az eredményt:

\begin{matrix} q_{1} = a_{1}^{5} - 5 a_{2} a_{1}^{3} + 5 a_{3} a_{1}^{2} + 5 a_{2}^{2} a_{1} - 5 a_{2} a_{3} . \end{matrix}

(2)

q_{2}

kiszámításához írjuk fel azt a

g_{2} (x) = x^{3} - b_{1} x^{2} + b_{2} x - b_{3}

polinomot, amelynek a gyökei éppen a g

_{1} (x)

gyökeiből készített kéttényezős szorzatok,

x_{1} x_{2}

x_{2} x_{3}

, illetve

x_{3} x_{1}

. A megoldásban látottak szerint ekkor

\begin{matrix} b_{1} & = x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} = a_{2}, \\ b_{2} & = x_{1} x_{2}^{2} x_{3} + x_{2} x_{3}^{2} x_{1} + x_{3} x_{1}^{2} x_{2} = x_{1} x_{2} x_{3} (x_{1} + x_{2} + x_{3}) = a_{1} a_{3}, végül \\ b_{3} & = x_{1} x_{2} x_{2} x_{3} x_{3} x_{1} = {(x_{1} x_{2} x_{3})}^{2} = a_{3}^{2} . \end{matrix}

Ezek után (2) alapján

q_{2} = b_{1}^{5} - 5 b_{2} b_{1}^{3} + 5 b_{3} b_{1}^{2} + 5 b_{2}^{2} b_{1} - 5 b_{2} b_{3}

, ahonnan behelyettesítés után

\begin{matrix} q_{2} = a_{2}^{5} - 5 a_{1} a_{3} a_{2}^{3} + 5 a_{3}^{2} a_{2}^{2} + 5 a_{1}^{2} a_{3}^{2} a_{2} - 5 a_{1} a_{3}^{3} . \end{matrix}

II. megoldás. Ha az

x^{3} + p x + q

polinom gyökei

x_{1}

x_{2}

és

x_{3}

, akkor egy szerencsés észrevétellel közvetlenül felírhatunk olyan egyenletet, amelynek éppen

x_{1}^{5}

x_{2}^{5}

és

x_{3}^{5}

a gyökei. Ha ugyanis az

\begin{matrix} x^{\frac{3}{5}} + p x^{\frac{1}{5}} + q \end{matrix}

kifejezésben

x

helyére

x_{i}^{5}

-t helyettesítünk, akkor

x_{i}^{3} + p x_{i} + q

adódik, ami a feltétel szerint nulla. Megfordítva, ha

y

megoldása az

x^{\frac{3}{5}} + p x^{\frac{1}{5}} + q = 0

egyenletnek, akkor ötödik gyöke polinomunknak lesz gyöke. A talált alak viszont sajnos nem polinom, de ezen lehet segíteni.
Használjuk fel az

\begin{matrix} {(a + b)}^{5} = a^{5} + b^{5} + 5 a b (a + b) (a^{2} + a b + b^{2}) \end{matrix}

azonosságot és emeljük ötödik hatványra az átrendezett

\begin{matrix} x_{i}^{\frac{3}{5}} + p x_{i}^{\frac{1}{5}} = - q \end{matrix}

(3)

egyenlőségeket (

i = 1,2,3

\begin{matrix} - q^{5} = x_{i}^{3} + p^{5} x_{i} + 5 p x_{i}^{\frac{4}{5}} (- q) (x_{i}^{\frac{6}{5}} + p x_{i}^{\frac{4}{5}} + p^{2} x_{i}^{\frac{2}{5}}) . \end{matrix}

A számolás során az

x_{i}^{\frac{3}{5}} + p x_{i}^{\frac{1}{5}}

összeget a vele (3) szerint egyenlő

(- q)

-val helyettesítettük. Ha most a zárójelben álló összegből kiemelünk

x_{i}^{\frac{1}{5}}

-t, akkor minden a helyére zökken, ugyanis (3) újabb fölhasználásával a megmaradt törtkitevők is eltüntethetők:

\begin{matrix} - q^{5} & = & x_{i}^{3} + p^{5} x_{i} - 5 p q x_{i} (x_{i} + p [{\underset{︸}{x_{i}^{\frac{3}{5}} + p x_{i}^{\frac{1}{5}}}}_{- q}^{}]), tehát \\ - q^{5} & = & x_{i}^{3} + p^{5} x_{i} - 5 p q x_{i} (x_{i} - p q) . \end{matrix}

A kapott egyenlőségek így azt jelentik, hogy

x_{i}^{5}

gyöke az

\begin{matrix} x^{3} - 5 p q x^{2} + (p^{5} + 5 p^{2} q^{2}) x + q^{5} = 0 \end{matrix}

egyenletnek. A feladatban

p = - 3

és

q = 1

, a keresett polinom tehát

\begin{matrix} x^{3} + 15 x^{2} - 198 x + 1, \end{matrix}

a = 15

b = - 198

c = 1

Megjegyzések. 1. Az olvasó általában is megkísérelheti a második megoldás módszerével közvetlenül felírni a megfelelő harmadfokú polinomot, amelynek együtthatói az I. megoldás általános formulái.
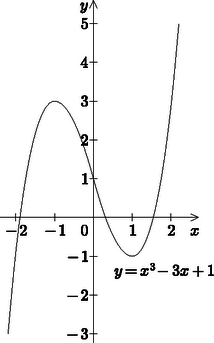
2. A hosszúra nyúlt megoldás végén magyarázattal szolgálhatunk a feladat némileg sajátos szövegezésére. Ha közelítő értékeket is elfogadhatónak tekintünk, akkor messze a legegyszerűbb út az eredeti egyenlet,

x^{3} - 3 x + 1 = 0

numerikus megoldása, hiszen a szóban forgó hatványösszegek azonnal számolhatók a gyökökből. A feladat nem kérdezte a gyökök jellegét, közöttük elvben komplex számok is lehetnek, ami persze nem befolyásolja a megoldást. Megnyugtatásul fölvázolhatjuk a függvény grafikonját (ábra): leolvasható, hogy az egyenletnek három valós gyöke van. Mivel egyikük sem racionális, csak a közelítő megoldás marad. A gyökök két tizedes pontossággal:

x_{1} \approx - 1, 88

;

x_{2} \approx 0, 35

;

x_{3} \approx 1, 53

. Ha ezekkel a közelítő értékekkel végezzük el a számolást, akkor két tizedesre kerekítve

x_{1}^{5} + x_{2}^{5} + x_{3}^{5} \approx - 15, 1

, illetve

(x_{1}^{5} x_{2}^{5}) + (x_{2}^{5} x_{3}^{5}) + (x_{3}^{5} x_{1}^{5}) \approx - 197

. Látható, hogy a második eredménynél a kerekítési hibák már egységnyi eltéréshez vezetnek, a számolás tehát legfeljebb az eredmény tesztelésére jó.

Egy másfajta, önmagában is érdekes megközelítéssel azonban igenis felírható a gyökök ,,pontos'' értéke. Ezt a módszert ‐ a modern algebrai jelölésrendszer kidolgozása mellett ‐ a nevezetes formulák névadója, François Vite dolgozta ki, éppen a harmadfokú egyenlet vizsgálata során. (Hozzátartozik az igazsághoz, hogy magukat a formulákat egy másik francia matematikus, Albert Girard vezette be a XVII. század első felében, egy jó emberöltővel Vite után.)
A matematikatörténet Vite-nek tulajdonítja az észrevételt, hogy a fenti típusú hiányos harmadfokú egyenletek kísértetiesen emlékeztetnek bizonyos jól ismert trigonometrikus összefüggésekre. Egyes források szerint azonban már az indiai matematikusok is használták ezt a módszert a XIV. században.
Ha a háromszoros szög szinuszára vonatkozó

sin 3 α = 3 sin α - 4 sin^{3} α

összefüggést 2-vel szorozzuk és átrendezzük, akkor az (1) egyenlethez hasonló szerkezetű alakot kapunk:

\begin{matrix} {(2 sin α)}^{3} - 3 \cdot (2 sin α) + 2 sin 3 α = 0. \end{matrix}

(1')

Ez az azonosság úgy is olvasható, hogy valahányszor az

α

szögre teljesül, hogy

(1')

utolsó tagja,

2 sin 3 α

egyenlő az (1) egyenlet konstans tagjával, ami most 1, akkor erre a szögre

2 sin α

az (1) egyenlet megoldása. Ez volt Vite észrevétele. Ezek után az (1) egyenlet gyökei a

\begin{matrix} 2 sin 3 α = 1 \end{matrix}

(4)

egyenlet megoldásával kaphatók. A (4) egyenlet megoldásai nyomban adódnak:

\begin{matrix} α = 10^{\circ} + k \cdot 120^{\circ}, illetve α = 50^{\circ} + k \cdot 120^{\circ} . \end{matrix}

A szinuszfüggvény szimmetriáit figyelembe véve három különböző szinusz-érték és így ‐ természetesen ‐ három különböző megoldás adódik: az (1) egyenlet gyökei tehát

2 sin 10^{\circ} \approx 0, 3473

;

2 sin 130^{\circ} \approx 1, 5321

, végül

2 sin 250^{\circ} \approx - 1, 8794

.
Ha tehát a szokásos módon a ,,Határozzuk meg az

a

b

c

számokat úgy, hogy

...

'' formában tűztük volna ki a feladatot, akkor, amint erre Csikvári Péter felhívta a figyelmünket, a fentiek alapján kifogástalan az alábbi válasz:

\begin{matrix} a & = & - 2^{5} (sin^{5} 10^{\circ} + sin^{5} 130^{\circ} + sin^{5} 250^{\circ}), \\ b & = & 2^{10} (sin^{5} 10^{\circ} \cdot sin^{5} 130^{\circ} + sin^{5} 130^{\circ} \cdot sin^{5} 250^{\circ} + sin^{5} 250^{\circ} \cdot sin^{5} 10^{\circ}), \\ c & = & - 2^{15} \cdot sin^{5} 10^{\circ} \cdot sin^{5} 130^{\circ} \cdot sin^{5} 250^{\circ} . \end{matrix}

A feladat szövegében szereplő érthetetlennek tűnő kitétel a tízes számrendszerbeli alakról éppen erről az útról akarta letéríteni Vite esetleges követőit. Valószínűleg maximális pontszámot kellett volna ajánlanunk, ha valaki így oldja meg a feladatot.