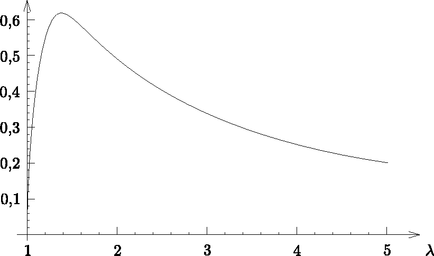Kezdőlap


Feladat:	2004. évi Nemzetközi Fizika Diákolimpia 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2004/november, 495 - 498. oldal		PDF \| MathML
Témakör(ök):	Gázok egyéb állapotváltozása, Egyéb nyújtás, összenyomás, Nemzetközi Fizika Diákolimpia
Hivatkozás(ok):	Feladatok: 2004/október: 2004. évi Nemzetközi Fizika Diákolimpia 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. feladat. Felemelkedő ballon
$(a)$ Felhasználva az ideális gáz állapotegyenletét, $n$ mól hélium gáz térfogata $p + Δ p$ nyomáson és $T$ hőmérsékleten

\begin{matrix} V = \frac{n R T}{p + Δ p}, \end{matrix}

míg

n'

mól levegő térfogata

p

nyomáson és

T

hőmérsékleten

\begin{matrix} V = \frac{n' R T}{p} . \end{matrix}

Így a ballon kiszorít

n' = n \frac{p}{p + Δ p}

mól levegőt, melynek súlya

M_{lev} n' g

. A kiszorított levegő súlya megegyezik a felhajtóerővel, azaz

\begin{matrix} F_{fel} = M_{lev} n g \frac{p}{p + Δ p} . \end{matrix}

(b)

z

magasságkülönbségből származó nyomásváltozás

- ϱ g z

, ha a levegő

ϱ

sűrűsége állandó. Ha a sűrűség a magasság függvényeként változik, akkor a következő egyenletet használhatjuk:

\begin{matrix} \frac{d p}{d z} = - ϱ g = - \frac{ϱ_{0} T_{0}}{p_{0}} \frac{p}{T} g, \end{matrix}

ahol az egyesített gáztörvényt

\frac{ϱ T}{p} = állandó

alakban használtuk. Ha ebbe az egyenletbe behelyettesítjük a feladatban megadott

p (z) = p_{0} {(1 - z / z_{0})}^{η}

összefüggést, illetve a

T (z) = T_{0} (1 - z / z_{0})

függvényt, akkor a deriválás elvégzése után a keresett

η

kitevőt így fejezhetjük ki:

\begin{matrix} η = \frac{ϱ_{0} z_{0} g}{p_{0}} = \frac{1, 16 \cdot 4, 9 \cdot 10^{4} \cdot 9, 8}{1, 01 \cdot 10^{5}} = 5, 52. \end{matrix}

A kérdéses kitevő számértéke tehát két értékes jegy pontossággal: 5,5.

(c)

Amikor

Δ p

nyomáskülönbség mellett a ballon sugarát

r

-ről

(r + d r)

-re növeljük, akkor a rugalmas megnyújtáshoz szükséges munka

\begin{matrix} d W = 4 π r^{2} Δ p d r, \end{matrix}

míg ugyanekkora

r

sugár mellett a rugalmas energia növekményét a feladatban megadott

U = 4 π r_{0}^{2} κ R T (2 λ^{2} + \frac{1}{λ^{4}} - 3)

energia függvény deriválásával határozhatjuk meg:

\begin{matrix} d W = (\frac{d U}{d r}) d r = 4 π κ R T (4 r - 4 \frac{r_{0}^{6}}{r^{5}}) d r . \end{matrix}

A munkavégzés kétféle kifejezésének egyenlővé tételével kaphatjuk meg a kívánt választ:

\begin{matrix} Δ p = 4 κ R T (\frac{1}{r} - \frac{r_{0}^{6}}{r^{7}}) = \frac{4 κ R T}{r_{0}} (\frac{1}{λ} - \frac{1}{λ^{7}}) . \end{matrix}

A nyomáskülönbség grafikon

λ

(

>

1) függvényében kezdetben élesen növekszik,

λ = 7^{1 / 6} = 1, 38

értéknél maximumot vesz fel, majd nagy

λ

értékeknél

λ^{- 1}

szerint csökken. A következő ábrán a dimenziótlan

\begin{matrix} \frac{Δ p}{\frac{4 κ R T}{r_{0}}} = (\frac{1}{λ} - \frac{1}{λ^{7}}) \end{matrix}

kifejezés ábrázolása látható:

(d)

Írjuk fel az ideális gáz állapotegyenletét:

p_{0} V_{0} = n_{0} R T_{0}

, ahol

V_{0}

a feszítetlen falú ballon térfogatát jelenti. Az

n

mól gázt tartalmazó ballon belső nyomása

V = λ^{3} V_{0}

térfogat mellett

T = T_{0}

hőmérsékleten:

\begin{matrix} p_{belső} = \frac{n R T_{0}}{V} = \frac{n}{n_{0} λ^{3}} p_{0} . \end{matrix}

Másrészt a ballon belső nyomását a

(c)

alkérdésre megadott többletnyomás segítségével is kifejezhetjük

T = T_{0}

hőmérsékleten:

\begin{matrix} p_{belső} = p_{0} + Δ p = p_{0} + \frac{4 κ R T_{0}}{r_{0}} (\frac{1}{λ} - \frac{1}{λ^{7}}) = [1 + a (\frac{1}{λ} - \frac{1}{λ^{7}})] p_{0} . \end{matrix}

A belső nyomás fenti két kifejezését egyenlővé téve határozhatjuk meg az

a

,,ballonparamétert'':

\begin{matrix} a = \frac{\frac{n}{n_{0} λ^{3}} - 1}{λ^{- 1} - λ^{- 7}} . \end{matrix}

A megadott

n / n_{0} = 3, 6

és

λ = 1, 5

numerikus adatokat behelyettesítve, a ballonparaméterre

a = 0, 11

adódik.

(e)

(a)

alkérdésben levezetett felhajtóerő egyensúlyt tart az

M_{teljes} = 1, 12

kg tömegre ható nehézségi erővel, ami a következő összefüggésre vezet:

\begin{matrix} \frac{p}{p + Δ p} = \frac{M_{teljes}}{M_{lev} \cdot n} . \end{matrix}

Másrészről, ha a

V = \frac{4}{3} π r^{3} = λ^{3} \frac{4}{3} π r_{0}^{3} = λ^{3} V_{0}

térfogatú ballon belsejében lévő héliumra újra alkalmazzuk az ideális gáz állapotegyenletét, akkor tetszőleges külső

p

nyomás és

T

hőmérséklet esetén a ballonban lévő

n

mól héliumra felírhatjuk:

\begin{matrix} (p + Δ p) λ^{3} = \frac{n R T}{V_{0}} = p_{0} \frac{T}{T_{0}} \frac{n}{n_{0}} . \end{matrix}

Ha a fenti két összefüggés mellett felhasználjuk a

(c)

alkérdésben a nyomáskülönbségre megkapott formulát, akkor meghatározhatjuk a három ismeretlen mennyiséget, vagyis

p

Δ p

és

λ

értékét mint a

T

hőmérséklet és egyéb adatok függvényét.
A fenti két összefüggés összevetéséből a felhajtóerő‐súly egyensúlyra egy újabb feltételt kapunk:

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ^{3} = \frac{M_{teljes}}{M_{lev} \cdot n_{0}} . \end{matrix}

Ezek után használjuk fel a

(c)

alkérdésben a nyomáskülönbségre megkapott formulát és az ideális gázegyenletből kapott összefüggést:

\begin{matrix} p λ^{3} + \frac{4 κ R T}{r_{0}} λ^{2} (1 - λ^{- 6}) = p_{0} \frac{T}{T_{0}} \frac{n}{n_{0}}, \end{matrix}

illetve ezt átrendezve és felhasználva a korábban bevezetett

a

,,ballonparamétert'':

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ^{3} = \frac{n}{n_{0}} - a λ^{2} (1 - λ^{- 6}) . \end{matrix}

Így az előzőleg a felhajtóerő-súly egyensúlyra kapott feltétellel megegyező bal oldalú összefüggésre jutottunk. A jobb oldalak egyenlővé tételével olyan egyenlethez juthatunk, amely már csak a

λ

lineáris méretnövekedési arányt tartalmazza:

\begin{matrix} λ^{2} (1 - λ^{- 6}) = \frac{1}{a n_{0}} (n - \frac{M_{teljes}}{M_{lev}}) = 4,54. \end{matrix}

Az egyenlet megoldása akkor egyszerű, ha közelítést (belátható, hogy nagyon jó közelítést) használunk:

\begin{matrix} λ^{2} \approx \frac{4, 54}{1 - 4, 54^{- 3}} \approx 4, 54 \to λ_{f} ≅ 2, 13. \end{matrix}

A ballon maximális emelkedési magasságát úgy kaphatjuk meg, ha a felhajtóerő‐súly egyensúlyra kapott feltételben

(\frac{p}{p_{0}} \frac{T_{0}}{T})

helyére beírjuk a nyomás és a hőmérséklet magasságfüggését, amit a

(b)

alkérdésben ismerhettünk meg:

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ_{f}^{3} = {(1 - \frac{z_{f}}{z_{0}})}^{η - 1} λ_{f}^{3} = \frac{M_{teljes}}{M_{lev} \cdot n_{0}} = 3, 10. \end{matrix}

Felhasználva, hogy

λ_{f} = 2, 13

és

(η - 1) = 4, 5

, a ballon maximális emelkedési magasságára

\begin{matrix} z_{f} = (49 km) \cdot (1 - {[\frac{3, 10}{2, 13^{3}}]}^{\frac{1}{4, 5}}) = 10, 9 km. \end{matrix}

A ballon tehát mintegy 11 km magasságra emelkedik, és lineáris mérete

λ_{f} = 2, 1

-szeresére növekszik.