Feladat: B.3718 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Antal László ,  Birkus Róbert ,  Csajbók Bence ,  Dobos Gábor ,  Eckert Bernadett ,  Erdélyi Márton ,  Estélyi István ,  G. Szabó Kálmán ,  Gyarmati Ákos ,  Hagymási Imre ,  Hartmann Zoltán ,  Hubai Tamás ,  Jankó Zsuzsanna ,  Kisfaludi-Bak Sándor ,  Kiss-Tóth Christián ,  Kórus Péter ,  Majoros Csilla ,  Nagy János ,  Pálinkás Csaba ,  Strenner Balázs ,  Vass Márton 
Füzet: 2004/október, 419 - 421. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Körülírt kör, Feuerbach-kör, Tengelyes tükrözés, Feladat
Hivatkozás(ok):Feladatok: 2004/március: B.3718

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mivel a középvonalak párhuzamosak az eredeti háromszög megfelelő oldalaival, az eredeti háromszög oldalfelező merőlegesei a középvonalak által alkotott háromszögben magasságvonalak. Vagyis az eredeti háromszög körülírható körének középpontja éppen a középvonalak által alkotott háromszög magasságpontja. Elegendő tehát a következő állítást belátnunk:

 
Egy háromszög magasságpontján áthaladó egyenesnek a háromszög oldalegyeneseire vett tükörképei egy ponton mennek át.
 
Jelöljük a háromszög csúcsait A, B, C-vel, szögeit a szokásos módon α, β, γ-val. Válasszuk úgy a jelölést, hogy 90∘>α≥β teljesüljön. A magasságpontot jelölje M, az ezen áthaladó adott egyenest h, ennek az oldalakra vonatkozó tükörképeit ha, hb és hc, M-nek az oldalegyenesekre vonatkozó tükörképeit pedig Ma, Mb és Mc. Mivel h átmegy M-en, azért hx átmegy Mx-en (x=a,b,c). Tudjuk továbbá (lásd pl. Geometriai feladatok gyűjteménye I., 1079. feladat), hogy az Mx pontok rajta vannak az ABC háromszög köré írt k körön.
 

 
1. ábra
 

 

 
2. ábra
 

A továbbiakban négy esetet különböztetünk meg. Ha γ=90∘ (1. ábra), akkor ha és hb egybeesik, az állítás nyilvánvaló. Ha γ hegyesszög, akkor a 2. ábrán, ha pedig γ tompaszög, akkor h helyzetétől függően a 3. vagy a 4. ábrán látható lehetőségeket kell vizsgálnunk. Mindhárom esetben igaz, hogy AC felezi az MbAM, AB pedig felezi az McAM szöget. Ezért MbAMc∢=2α (mert MbAMc∢=2⋅McAM∢±2⋅MbAM∢=2⋅CAB∢). Ha a hc egyenest előbb az AB, majd a képét az AC egyenesre tükrözzük, akkor a hb egyenest kapjuk, hiszen az első tükrözésnél hc képe h. Viszont a két tükrözés egymásutánja megegyezik egy A körüli 2⋅BAC∢=2α szögű elforgatással. Tehát hc-t hb-be egy 2α szögű elforgatás viszi. Ezért a két egyenes egymással 2α (vagy 2α>90∘ esetén 180∘-2α) szöget zár be. Ha a két egyenes metszéspontját P jelöli, akkor az egyes eseteknek megfelelően azt kapjuk, hogy MbPMc∢=180∘-2α (2. ábra), illetve MbPMc∢=2α (3. és 4. ábra). Tehát P minden esetben rajta van az MbAMc háromszög köré írt körön. Ez a kör egyúttal az ABC háromszög köré írt köre is, azaz megegyezik k-val. Ugyanígy láthatjuk be, hogy hc és ha metszéspontja ‐ jelöljük Q-val ‐ is rajta van a k 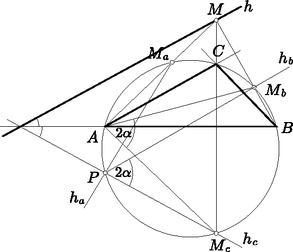körön.
 

 
3. ábra
 

 

 
4. ábra
 

Ha P egybeesik Mc-vel, akkor hb megegyezik az MbMc egyenessel. A kerületi szögek tétele miatt McMbB∢=McCB∢=90∘-β, ezért az AC oldallal hb is, és így h is β szöget zár be (5., ill. 6. ábra). Tehát az AB oldallal h is, és így hc is α-β szöget zár be. Ezért hc az AB-re merőleges CM egyenessel 90∘-(α-β) szöget zár be. A kerületi szögek tétele miatt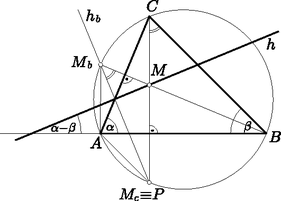
McBC∢=McBA∢+ABC∢=McCA∢+β=90∘-α+β,
ezért az A-t tartalmazó McC ívhez tartozó kerületi szög megegyezik hc és McC szögével, hc tehát Mc-ben érinti k-t. Ebből viszont következik, hogy Q is egybeesik Mc-vel, tehát ebben az esetben igaz az állításunk. Ugyanígy látható be az állítás abban az esetben is, ha azt tesszük fel, hogy Q esik egybe Mc-vel.
 

 
5. ábra
 

 

 
6. ábra
 

Ha viszont se P, se Q nem esik egybe Mc-vel, akkor mindkettőjüknek egybe kell esnie hc és k Mc-től különböző metszéspontjával, tehát állításunk ekkor is igaz.
Eredeti állításunknál többet is bizonyítottunk. Mivel azt is megmutattuk, hogy a ha, hb és hc egyenesek közös pontja mindig rajta van k-n, azért az eredeti feladatban szereplő tükörképek közös pontja rajta van a háromszög középvonalai által alkotott háromszög köré írt körön, ami nem más, mint az eredeti háromszög Feuerbach-köre.