Kezdőlap


Feladat:	B.3710	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antal László , Bereczki Péter , Birkus Róbert , Bittner Emese , Bogár Péter , Csajbók Bence , Cseh Ágnes , Csizmadia János , Dobos Gábor , Eckert Bernadett , Erdélyi Márton , Estélyi István , Fehér Gábor , Gehér György , Gyarmati Ákos , Hegyháti Máté , Holló László , Hubai Tamás , Hujter Bálint , Jankó Zsuzsanna , Kisfaludi-Bak Sándor , Kiss-Tóth Christián , Koszta Botond , Kovács Péter , Kunovszki Péter , Kurgyis Zsuzsanna , Lorántfy Bettina , Molnár András , Nagy Csaba , Nagy Péter , Nagy-Baló András , Pálinkás Csaba , Pálovics Róbert , Poronyi Balázs , Prónai Anett , Strenner Balázs , Sümegi Károly , Varga Viktor
Füzet:	2004/október, 417 - 419. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Szögfelező egyenes, Síkgeometriai bizonyítások, Párhuzamos szelők tétele és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 2004/február: B.3710

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tudjuk, hogy egy hegyesszögű háromszög magasságvonalai egyúttal a talpponti háromszög belső szögfelezői is (ennek bizonyítása megtalálható pl. a Geometriai feladatok gyűjteménye I. kötetének 1060. feladatában). Ezért a $T_{1} T_{2} T_{3}$ háromszög $T_{i}$ csúcsához tartozó belső szögfelezője a $T_{i} A_{i}$ egyenes, s így a külső szögfelező az erre merőleges $A_{j} A_{k}$ egyenes (ahol 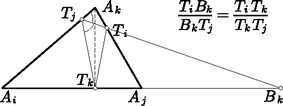${i; j; k} = {1; 2; 3}$ ).
A külső szögfelező tétel szerint a szögfelező az őt közrefogó oldalak arányában osztja a szemközti oldalt, vagyis

\begin{matrix} \frac{T_{1} B_{3}}{B_{3} T_{2}} = \frac{T_{1} T_{3}}{T_{3} T_{2}}, \frac{T_{2} B_{1}}{B_{1} T_{3}} = \frac{T_{2} T_{1}}{T_{1} T_{3}} és \frac{T_{3} B_{2}}{B_{2} T_{1}} = \frac{T_{3} T_{2}}{T_{2} T_{1}} . \end{matrix}

Tehát

\begin{matrix} \frac{T_{1} B_{3}}{B_{3} T_{2}} \cdot \frac{T_{2} B_{1}}{B_{1} T_{3}} \cdot \frac{T_{3} B_{2}}{B_{2} T_{1}} = \frac{T_{1} T_{3}}{T_{3} T_{2}} \cdot \frac{T_{2} T_{1}}{T_{1} T_{3}} \cdot \frac{T_{3} T_{2}}{T_{2} T_{1}} = 1. \end{matrix}

1. ábra

Azonban a

B_{i}

pontok nem a

T_{j} T_{k}

oldalszakaszokon, hanem azok meghosszabbításain fekszenek, ezért ha előjeles szakaszokkal számolunk, akkor azt kapjuk, hogy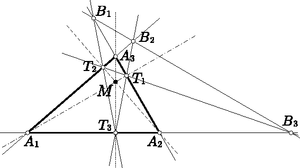

\begin{matrix} \frac{T_{1} B_{3}}{B_{3} T_{2}} \cdot \frac{T_{2} B_{1}}{B_{1} T_{3}} \cdot \frac{T_{3} B_{2}}{B_{2} T_{1}} = - 1. \end{matrix}

Ez pedig Menelaosz tételének megfordítása szerint (lásd pl. Geometriai feladatok gyűjteménye I; 1261. feladat) azt jelenti, hogy a

B_{1}

B_{2}

B_{3}

pontok egy egyenesen vannak, ami éppen a bizonyítandó állítás.

II. megoldás. Az

A_{1} A_{2} A_{3}

és

T_{1} T_{2} T_{3}

háromszögek megfelelő csúcsait összekötő egyenesek egy ponton, az

A_{1} A_{2} A_{3}

háromszög magasságpontján mennek át (2. ábra). Ezért Desargues tételéből (lásd pl. Schmidt Tamás: Geometriai terek az algebra szemszögéből, lapunk 2004. évi 4. számának 199‐206. oldalain) következik, hogy a két háromszög megfelelő oldalegyeneseinek metszéspontjai egy egyenesen vannak. Mivel

B_{i}

éppen

A_{j} A_{k} \cap T_{j} T_{k}

(ahol

{i; j; k} = {1; 2; 3}

), a

B_{1}

B_{2}

B_{3}

pontok egy egyenesen vannak.

2. ábra

Megjegyzés. A második megoldás során nem használtuk ki, hogy a

T_{i}

pontok a magasságok talppontjai. Az állítás minden olyan

T_{1} T_{2} T_{3}

háromszög esetén igaz, amelyre teljesül, hogy az

A_{i} T_{i}

(i = 1,2,3)

egyenesek egy ponton mennek át.