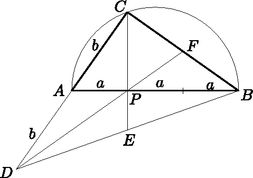
I. megoldás. Létezik olyan háromszög, ahol a súlyvonalak által meghatározott egyik háromszög hasonló az eredetihez. Először megadjuk a konstrukciót a háromszög szerkesztésével, majd belátjuk, hogy ez jó.
Felveszünk egy $AB$ szakaszt, azt elharmadoljuk és megszerkesztjük a Thalész-körét. Az egyik harmadolópontból, $P$-ből, merőlegest állítunk $AB$-re, ennek metszéspontja a körrel $C$. $ACB\sphericalangle ={90}^{\circ }$, mert $C$ rajta van $AB$ Thalész-körén. $AC$-t meghosszabítjuk $A$-n túl a saját hosszával, a szakasz végpontja legyen $D$. A $CP$ egyenes és a $DB$ szakasz metszéspontja legyen $E$. A $DBC$ háromszögnek $AB$ súlyvonala, mivel $AC=AD$. $CE$ is súlyvonala a $DBC$ háromszögnek, mert a másik súlyvonalnak, $AB$-nek a megfelelő harmadolópontján halad át. Az $APC$ háromszög tehát a $DBC$ háromszög súlyvonalai által meghatározott egyik háromszög.

DE=EC(=EB), azaz a $DEC$ háromszög egyenlő szárú, így $CDE\sphericalangle =ECD\sphericalangle$. Tehát az $APC$ háromszög és a $DCB$ háromszög két szöge megegyezik, vagyis a két háromszög valóban hasonló.

 

Megjegyzés. A hasonlóságot és néhány Pitagorasz-tételt felírva kevés számolás után meghatározható, hogy a $DCB$ háromszög oldalainak aránya $1:\sqrt[]{2}:\sqrt[]{3}$.

 

II. megoldás. Válasszuk ki tetszőlegesen az egyik kis háromszöget a hat közül ($AGS▵$). Vizsgáljuk meg, hogy a nagy háromszög oldalainak hosszára milyen feltételt jelent e két háromszög hasonlósága. Felhasználjuk a súlypont harmadoló tulajdonságát. Tudjuk továbbá, hogy minden ilyen kis háromszögnek a területe $\frac{1}{6}$-a a nagy háromszög területének. Így hasonlóság csak $\frac{1}{\sqrt[]{6}}$ aránnyal teljesülhet. Ebből az is következik, hogy az $ABC$ háromszög $c$ oldalának nem lehet az $AGS$ háromszög $AG=\frac{c}{2}$ oldala a megfelelője.

 

 

A szögeket figyelve észrevehetjük, hogy $GAS\sphericalangle <\alpha$, így a $GS=\frac{s_c}{3}$ oldal nem lehet a nagy háromszög $a$ oldalának a képe. Valamint $GC$ nyilván nem párhuzamos $BC$-vel, így $AGC\sphericalangle \ne \beta$, tehát az $AS=\frac{2s_a}{3}$ nem lehet a nagy háromszög $b$ oldalának a képe.
Két lehetőségünk maradt:

${\displaystyle \begin{array}{ccccccc}\hfill {\displaystyle \frac{c}{2}}& {\displaystyle =a\text{'}=\frac{1}{\sqrt[]{6}}\cdot a\mathrm{,}}\hfill & {\displaystyle \frac{s_c}{3}}\hfill & \hfill {\displaystyle =b\text{'}=\frac{1}{\sqrt[]{6}}\cdot b\mathrm{,}}& {\displaystyle \frac{2s_a}{3}}\hfill & {\displaystyle =c\text{'}=\frac{1}{\sqrt[]{6}}\cdot c\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle \frac{c}{2}}& {\displaystyle =b\text{'}=\frac{1}{\sqrt[]{6}}\cdot b\mathrm{,}}\hfill & {\displaystyle \frac{s_c}{3}}\hfill & \hfill {\displaystyle =c\text{'}=\frac{1}{\sqrt[]{6}}\cdot c\mathrm{,}}& {\displaystyle \frac{2s_a}{3}}\hfill & {\displaystyle =a\text{'}=\frac{1}{\sqrt[]{6}}\cdot a\mathrm{.}}\hfill & \text{(<mi>*</mi>)}\end{array}}$

Mivel a súlyvonalak hosszát ki tudjuk fejezni a háromszög oldalhosszainak a segítségével, így már csak az a dolgunk, hogy megvizsgáljuk, hogy az $a^2$, $b^2$, $c^2$-re kapott elsőfokú egyenletrendszer nem vezet-e ellentmondáshoz. Ha nem vezet, akkor létezik ilyen háromszög, mellesleg meg fogjuk kapni oldalainak arányát. Ha ellentmondásra vezet, akkor pedig nem létezik ilyen háromszög.
Kezdjük:
${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}{\displaystyle \left(1a\right)}\hfill & \hfill {\displaystyle \frac{c^2}{4}}& {\displaystyle =\frac{a^2}{6}\mathrm{,}}\hfill \\ {\displaystyle \left(2a\right)}\hfill & \hfill {\displaystyle \frac{s_c^2}{9}}& {\displaystyle =\frac{b^2}{6}\mathrm{,}}\hfill & \hfill {\displaystyle s_c^2}& {\displaystyle =\frac{2a^2+2b^2-c^2}{4}\mathrm{,}}\hfill \\ {\displaystyle \left(3a\right)}\hfill & \hfill {\displaystyle \frac{4s_a^2}{9}}& {\displaystyle =\frac{c^2}{6}\mathrm{,}}\hfill & \hfill {\displaystyle 4s_a^2}& {\displaystyle =2b^2+2c^2-a^2;}\hfill \end{array}}\}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle \Downarrow }\hfill \\ \hfill {\displaystyle \left(1b\right)3c^2=2a^2\mathrm{,}\left(2b\right)\frac{2a^2+2b^2-c^2}{4\cdot 9}=\frac{b^2}{6}\mathrm{,}\left(3b\right)\frac{2b^2+2c^2-a^2}{9}=\frac{c^2}{6};}\hfill \\ \hfill {\displaystyle \Downarrow }\hfill \\ \hfill {\displaystyle \left(1c\right)3c^2=2a^2\mathrm{,}\left(2c\right)2a^2+2b^2-c^2=6b^2\mathrm{,}\left(3c\right)4b^2+4c^2-2a^2=3c^2;}\hfill \\ \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>1</mn><mi>c</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>-t írjuk be a <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mi>c</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> és a <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>3</mn><mi>c</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> egyenletbe is:}}\hfill \\ \hfill {\displaystyle \left(2d\right)3c^2+2b^2-c^2=6b^2\mathrm{,}\left(3d\right)4b^2+4c^2-3c^2=3c^2;}\hfill \\ \hfill {\displaystyle \Downarrow }\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(2e\right)2c^2=4b^2}\hfill \\ \hfill {\displaystyle \left(3e\right)4b^2=2c^2}\hfill \end{array}}\}{\displaystyle \begin{array}{c}{\displaystyle \text{A két egyenlet ekvivalens,}}\hfill \\ {\displaystyle \text{nem kaptunk tehát ellentmondást.}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{c}{\displaystyle 3c^2=2a^2=6b^2}\hfill \\ {\displaystyle \frac{c^2}{2}=\frac{a^2}{3}=b^2}\hfill \\ {\displaystyle \frac{c}{\sqrt[]{2}}=\frac{a}{\sqrt[]{3}}=b\mathrm{,}}\hfill \end{array}}}\hfill \end{array}}$

vagyis az oldalak aránya ebben az esetben $a:b:c=\sqrt[]{3}:1:\sqrt[]{2}$.

$\begin{array}{cc}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{c^2}{4}}& {\displaystyle =\frac{b^2}{6}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{s_c^2}{9}}& {\displaystyle =\frac{c^2}{6}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{4s_a^2}{9}}& {\displaystyle =\frac{a^2}{6};}\hfill \end{array}}\}{\displaystyle \begin{array}{c}{\displaystyle \text{Az előzőhöz hasonlóan végül két ekvivalens egyenlethez}}\hfill \\ {\displaystyle \text{jutunk. Itt <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>6</mn><mrow><msup><mrow><mi>c</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>4</mn><mrow><msup><mrow><mi>b</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, amiből <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">:</mo><mi>b</mi><mo stretchy="false">:</mo><mi>c</mi><mo stretchy="false">=</mo><mn>2</mn><mo stretchy="false">:</mo><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow><mo stretchy="false">:</mo><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></math>.}}\hfill \end{array}}}& \hfill {\displaystyle (\text{*})}\\ {\displaystyle }\end{array}$

Ezzel az összes lehetséges háromszöget megkaptuk. Az I. eset az első megoldásban megadott derékszögű háromszöget szolgáltatta. A II. esetbeli háromszög nem derékszögű, így lényegesen ritkábban bukkant föl a dolgozatokban.