| Feladat: | B.3696 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bednay Dezső , Csajbók Bence , Filus Tamás , Gehér György , Hannák Gábor , Hubai Tamás , Kiss-Tóth Christián , Kőrizs Beatrix , Kovács Péter , Kunovszki Péter , Nagy Csaba , Nándori Péter , Nikházy László , Pálinkás Csaba , Stippinger Marcell , Strenner Balázs , Szabó Botond , Szabó Tamás , Szalóki Dávid , Szilágyi Dániel , Udvari Balázs , Ureczky Bálint | ||
| Füzet: | 2004/október, 415. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkbeli ponthalmazok távolsága, Indirekt bizonyítási mód, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2004/január: B.3696 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Az egyszerűség kedvéért azonosítsuk az egyenest a számegyenessel. Ekkor mindegyik félegyenes vagy ,,jobbra végtelen'' (azaz a -t tartalmazza), vagy ,,balra végtelen'' (azaz a -t tartalmazza). A pontosan számú félegyenes által lefedett részek -félék lehetnek aszerint, hogy hány jobbra végtelen félegyenes tartalmazza őket (mert ezen félegyenesek száma legalább és legfeljebb ). 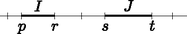 Ha viszont a két rész és , ahol a jelölést úgy választjuk, hogy , (lásd az ábrát), akkor minden -t tartalmazó jobbra nyílt félegyenes -t is tartalmazza, míg minden -t tartalmazó balra nyílt félegyenes -t is tartalmazza. Ezért nem lehet az adott félegyenesek közt olyan, amelynek kezdőpontja az zárt intervallumba esik, mert ez a félegyenes és közül csak pontosan az egyiket tartalmazná. Tehát ellentmondásra jutottunk, s ezzel a bizonyítást befejeztük. |