Kezdőlap


Feladat:	B.3691	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antal László , Bednay Dezső , Birkner Tamás , Birkus Róbert , Bitai Tamás , Bodnár József , Bogár Péter , Bogya Norbert , Estélyi István , Hegyháti Máté , Hubai Tamás , Hujter Bálint , Jankó Zsuzsanna , Károlyi Márton , Kiss-Tóth Christián , Kurgyis Zsuzsanna , Lorántfy Bettina , Magda Gábor , Matyuska Ferenc , Nándori Péter , Poronyi Balázs , Stippinger Marcell , Strenner Balázs , Szalóki Dávid , Vaskó Richárd , Vass Márton
Füzet:	2004/október, 412 - 413. oldal		PDF \| MathML
Témakör(ök):	Téglatest, Vetítések, Terület, felszín, Szélsőérték-feladatok, Feladat
Hivatkozás(ok):	Feladatok: 2003/december: B.3691

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Merőleges vetítésnél konvex halmaz képe konvex halmaz, párhuzamos és egyenlő hosszú szakaszok képei pedig párhuzamosak és egyenlő hosszúak (egymással nem párhuzamos, de egyenlő hosszú szakaszok képei persze általában nem egyenlő hosszúak). Ezért, ha a $T$ téglatestet vetítjük, a vetület olyan konvex síkidom lesz, amely középpontosan szimmetrikus, és amelyet $T$ bizonyos éleinek vetületei határolnak. $T$ élei 3 csoportba oszthatók úgy, hogy minden egyes csoportban 4 egymással párhuzamos, egyenlő hosszúságú él szerepel. Mivel egy konvex síkidomnak legfeljebb két darab, ugyanazzal az egyenessel párhuzamos oldala lehet, azért $T$ merőleges vetülete olyan középpontosan szimmetrikus hatszög, melynek határoló élei mindhárom csoportból két-két alkalmas él vetületeként jönnek létre, s az egymással szemközti oldalai rendre $T$ különböző hosszúságú éleinek vetületeként adódnak (1. ábra, $P'$ jelöli a $P$ pont merőleges vetületét). Ha a vetítés olyan egyenes mentén történik, amely nem párhuzamos $T$ egyik lapsíkjával sem, akkor a vetület valódi hatszög, ha pedig a vetítés nem ilyen egyenes mentén történik, akkor a hatszög elfajuló (ilyen látható a 2. ábrán).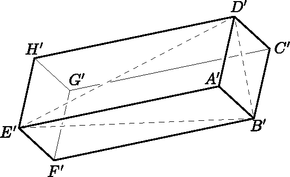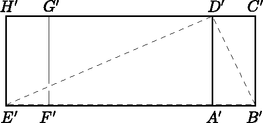

1. ábra

2. ábra

Választhatjuk

T

csúcsainak jelölését úgy, hogy a merőleges vetületnek

A'

és

G'

ne legyen csúcsa. Ekkor a

B' C' D' H' E' F'

(esetleg elfajuló) vetületi hatszöget az

A' B'

A' D'

és

A' E'

szakaszok paralelogrammákra bontják. E paralelogrammák területét a

B' D'

D' E'

és

E' B'

átlók rendre felezik, ezért a

B' D' E'

háromszög területe éppen fele a

T

vetületeként adódó hatszög területének.
A

B D E

háromszög oldalai

T

lapátlói. A lapátlók hossza a Pitagorasz-tétel alapján

\begin{matrix} e = \sqrt[]{3^{2} + 4^{2}} = 5, f = \sqrt[]{3^{2} + 12^{2}} = \sqrt[]{153} és g = \sqrt[]{4^{2} + 12^{2}} = \sqrt[]{160} . \end{matrix}

B' D' E'

háromszög területe nem lehet nagyobb a

B D E

háromszög

t

területénél, melyet a Héron-képlet alapján kiszámolhatunk:

\begin{matrix} t & = & \sqrt[]{\frac{e + f + g}{2} \cdot \frac{e + f - g}{2} \cdot \frac{e - f + g}{2} \cdot \frac{- e + f + g}{2}} = \\ = & \frac{1}{4} \sqrt[]{({(e + f)}^{2} - g^{2}) (g^{2} - {(e - f)}^{2})} = \\ = & \frac{1}{4} \sqrt[]{(10 \sqrt[]{153} + 18) (10 \sqrt[]{153} - 18)} = \frac{1}{4} \sqrt[]{15 300 - 324} = 6 \sqrt[]{26} . \end{matrix}

Tehát

T

merőleges vetületének területe nem lehet nagyobb, mint

12 \sqrt[]{26}

, ami el is érhető, ha a téglatestet egy olyan síkra vetítjük, amely párhuzamos

T

valamely két, közös csúcsból kiinduló lapátlójával.