Kezdőlap


Feladat:	2003. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kocsis Albert Tihamér
Füzet:	2004/október, 392 - 394. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Középponti és kerületi szögek, Szögfelező egyenes, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 2004/szeptember: 2003. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kocsis Albert Tihamér megoldása. Először azt látjuk be, hogy ha $A B C D$ húrnégyszög, akkor $P A = P C$ .
Legyen $B P$ és a kör metszéspontja $D'$ , $D P$ és a kör metszéspontja pedig $B'$ (1. ábra).

1. ábra

A B D ∢ = D' B C ∢

, az

{A D}_{}^{_{⌢}} = {D' C}_{}^{_{⌢}}

ívekhez tartozó kerületi szögek egyenlők, így

D

és

D'

A C

felező merőlegesére tükrösek. Ekkor a

B D'

és a

B' D

egyenesek is tükrösek erre a felező merőlegesre, a metszéspontjuk,

P

tehát rajta van az

A C

felező merőlegesén és így valóban

P A = P C

.
A megfordításhoz legyen

P A = P C

. Belátjuk, hogy a feladat feltételei mellett

A B C D

húrnégyszög. Először egy segédtételre lesz szükségünk:
Ha adott egy

X Y Z

háromszög és a síkjában egy

Q

pont, akkor a háromszög csúcsait a

Q

-val összekötő egyeneseknek az adott csúcson átmenő belső szögfelezőkre vonatkozó tükörképei egy ponton haladnak át (esetleg párhuzamosak). A bizonyítás megtalálható például Reiman István ‐ Dobos Sándor: Nemzetközi Matematikai Diákolimpiák (1959‐2003) (Typotex Kiadó, Budapest) c. könyvének függelékében.
Most a

B P D

háromszög játssza az

X Y Z

háromszög szerepét, a

Q

pontét pedig az

A

pont.

D A

tükörképe a

P D B

szög felezőjére éppen a

D C

egyenes, míg a

B A

tükörképe a

D B P

szög felezőjére a

B C

egyenes. Ez a két egyenes most a

C

pontban metszi egymást, így a

P A

egyenesnek a

D P B

szög felezőjére vonatkozó tükörképe a segédtétel állítása szerint átmegy a

C

ponton (2. ábra). Ez a tükörkép tehát a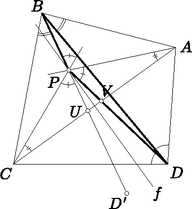

C P

egyenes.

2. ábra

Ekkor

A P B ∢ = 180^{\circ} - D P C ∢

, így ha

U = P B \cap A C

és

V = D P \cap A C

, akkor

V P C ∢ = A P U ∢

. Miután a feltétel szerint

P A = P C

, továbbá

P A U ∢ = P C V ∢

, így

P U V ∢ = P V U ∢

, a

P U V

háromszög egyenlő szárú. Jelölje az

A C

felező merőlegesét

f

.
Ekkor

P D

és

P B

tükrösek

f

-re, ez ugyanis a

P U V

háromszög szimmetriatengelye, a

P D

és

P B

egyenesek pedig a szárai.
Legyen a

D

csúcs tükörképe

f

-re

D'

. Az előbbi szimmetria miatt

D'

illeszkedik a

P B

egyenesre. A feltétel miatt

A B D ∢ = D' B C ∢

, tehát az

A D D' C

szimmetrikus trapézban az egyenlő hosszú

A D

és

D' C

szakaszok a

B

pontból egyenlő szögben látszanak. Az

A D

szakasz

A B D

szögű látóköre és a

D' C

szakasz

D' B C

szögű látóköre tehát egybevágó, másrészt ez a két kör is szimmetrikus az

f

-re. Ha egybeesnek, akkor

B

rajta van ezen a körön, amely egyébként a szimmetrikus

A D D' C

trapéz körülírt köre és készen vagyunk,

A B C D

húrnégyszög.
Ha a két látókör nem esik egybe, akkor

B

metszéspontjuk rajta van a két kör

f

szimmetriatengelyén. A fenti gondolatmenetet az

A D C

helyett az

A B C

háromszögre és a megfelelő

B'

pontra megismételve kapjuk, hogy ha a négy pont,

A

B

C

D

nincs egy körön, akkor

D

is rajta van az

f

egyenesen. Ha tehát nem igaz az állítás, akkor

B D

A C

átló felezőmerőlegese, az

A B C D

négyszög deltoid,

B D

felezi mind az

A D C

, mind pedig az

A B C

szöget. Ezt viszont a feltétel kizárja, az adott feltételek esetén tehát

A B C D

valóban húrnégyszög.